Giải SBT Toán 8 Chân trời sáng tạo Bài 2. Toạ độ của một điểm và đồ thị của hàm số có đáp án
23 người thi tuần này 4.6 445 lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
10.3 K lượt thi
10 câu hỏi
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
15.7 K lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
2.5 K lượt thi
21 câu hỏi
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
4 K lượt thi
10 câu hỏi
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
5.1 K lượt thi
10 câu hỏi
Bộ 10 đề thi Cuối kì 1 Toán 8 Kết nối tri thức có đáp án - Đề 1
13.7 K lượt thi
18 câu hỏi
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
1.6 K lượt thi
20 câu hỏi
Bộ 5 đề thi giữa kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
1 K lượt thi
20 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Lời giải
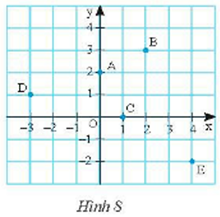
Dựa vào mặt phẳng toạ độ Oxy ở Hình 8, ta xác định được toạ độ các điểm là:
A(0; 2), B(2; 3), C(1; 0), D(–3; 1), E(4; –2).
Vậy toạ độ các điểm là A(0; 2), B(2; 3), C(1; 0), D(–3; 1), E(4; –2).
Lời giải
Lời giải
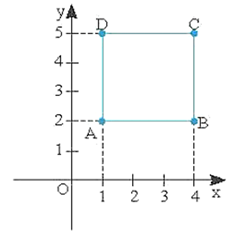
Vẽ mặt phẳng toạ độ Oxy và xác định các điểm A(1; 2), B(4; 2), C(4; 5) trên mặt phẳng
Để ABCD là hình vuông thì AD ^ AB và AD = AB = BC = CD = 3.
Do đó xác định được điểm D trên mặt phẳng toạ độ Oxy là D(1; 5).
Vậy toạ độ đỉnh D là D(1; 5).
Lời giải
Lời giải
a) Điểm M nằm trên trục tung nên hoành độ xM = 0.
Điểm M có tung độ là 3 hay yM = 3.
Vậy toạ độ điểm M là M(0; 3).
b) Điểm N nằm trên trục hoành nên tung độ yM = 0.
Điểm N có hoành độ là –6 hay xM = –6.
Vậy toạ độ điểm N là M(–6; 0).
c) Điểm O là gốc toạ độ nên có toạ độ là O(0; 0).
Lời giải
Lời giải
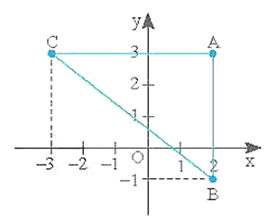
Ta vẽ hệ trục toạ độ Oxy và đánh dấu các điểm A(2; 3), B(2; –1), C(–3; 3).
Dựa vào mặt phẳng toạ độ ta thấy AB ^ AC nên tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
\[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.5 = 10\] (đvdt)
Lời giải
Lời giải
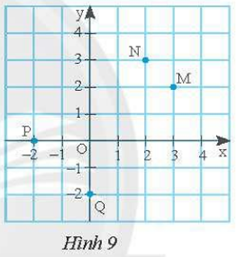
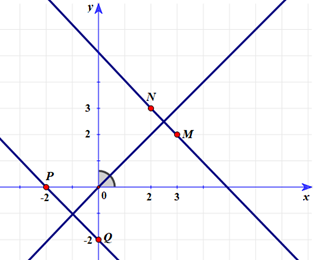
a) Dựa vào mặt phẳng toạ độ Oxy trong Hình 9 ta xác định được toạ độ các điểm là:
M(3; 2), N(2; 3), P(–2; 0) và Q(0; –2).
b) Các đoạn thẳng MN và PQ đều nhận tia phân giác của góc \[\widehat {xOy}\] làm trục đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập