Câu hỏi:

29/07/2022 4,140

Trong không gian Oxyz, cho mặt cầu $(C) : {(x + 1)}^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 1$ và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?

A. 6

B. 4

C. 2

D. 1

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Mặt cầu và mặt phẳng !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Bước 1:

Dễ dàng nhận thấy O,A,B đều nằm ngoài mặt cầu (C) nên (OAB) không cắt mặt cầu (C).

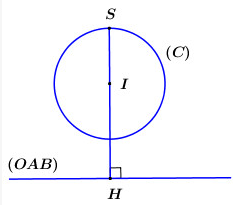
Mặt cầu (C) ta có tâm I(−1;3;2), bán kính R=1.

Ta có $\vec{O A} = (2; 1; 0), \vec{O B} = (0; 2; 0) \Rightarrow [\vec{O A}; \vec{O B}] = (0; 0; 4)$

$\Rightarrow S_{Δ O A B} = \frac{1}{2} |[\vec{O A}; \vec{O B}]| = 2$

Bước 2:

$\Rightarrow V_{S . O A B} = \frac{1}{3} d (S; (O A B)) . S_{Δ O A B}$

Vì $S_{Δ O A B}$ không đổi nên $V_{S . O A B}$ đạt giá trị lớn nhất khi và chỉ khi
$d (S; (O A B))$ lớn nhất, khi đó $d (S; (O A B)) = R + d (I; (O A B))$

Bước 3:

Mặt phẳng (OAB) nhận $\vec{n} = \frac{1}{4} [\vec{O A}; \vec{O B}] = (0; 0; 1)$ là 1 VTPT nên có phương trình: z = 0.

$\Rightarrow d (I; (O A B)) = |z_{I}| = 2 \Rightarrow d {(S; (O A B))}_{\max} = 1 + 2 = 3$

Vậy $\max V_{S . O A B} = \frac{1}{3} .3.2 = 2$

Đáp án cần chọn là: C

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian vớ hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;−1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. $x + y - 3 z - 8 = 0$

B. $x - y - 3 z + 3 = 0$

C. $x + y + 3 z - 9 = 0$

x + y - 3 z + 3 = 0

Lời giải

(P) là mặt phẳng tiếp xúc với (S) tại A nếu và chỉ nếu (P) đi qua A và $\vec{I A} ⊥ (P)$

Ta có: $\vec{I A} = (- 1; - 1; 3)$ là vec tơ pháp tuyến của mặt phẳng (P).

Mà (P) lại đi qua A(2;1;2) nên: $(P) : - 1 (x - 2) - 1 (y - 1) + 3 (z - 2) = 0 \Leftrightarrow x + y - 3 z + 3 = 0$

Đáp án cần chọn là: D

Câu 2

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : 2 x - y - 2 z - 2 = 0$ và mặt phẳng $(Q) : 2 x - y - 2 z + 10 = 0$ song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó

A. $r = \frac{2 \sqrt{5}}{3}$

B. $r = \frac{4 \sqrt{2}}{3}$

C. $r = \frac{2 \sqrt{2}}{3}$

r = \frac{\sqrt{5}}{3}

Lời giải

Media VietJack

Bước 1: Tính $d ((P), (Q))$

Ta thấy M(1;0;0) là một điểm thuộc (P)

Vì $(P) / / (Q)$ nên $d ((P), (Q)) = d (M, (Q)) = \frac{| 2 + 10 |}{\sqrt{2^{2} + {(- 1)}^{2} + {(- 2)}^{2}}} = 4$

Bước 2: Giả sử I(a;b;c) là tâm của (S). Chứng minh I luôn thuộc mặt phẳng (R)

Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là

$R = \frac{d ((P), (Q))}{2} = \frac{4}{2} = 2$

Do đó IA=2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2

Ngoài ra,

$d (I, (P)) = d (I, (Q)) \Leftrightarrow \frac{| 2 a - b - 2 c - 2 |}{\sqrt{2^{2} + {(- 1)}^{2} + {(- 2)}^{2}}} = \frac{| 2 a - b - 2 c + 10 |}{\sqrt{2^{2} + {(- 1)}^{2} + {(- 2)}^{2}}}$

$\Leftrightarrow | 2 a - b - 2 c - 2 | = | 2 a - b - 2 c + 10 |$

$\Leftrightarrow 2 a - b - 2 c + 4 = 0.$

Do đó, I luôn thuộc mặt phẳng $(R) : 2 x - y - 2 z + 4$

Bước 3: Gọi H là hình chiếu vuông góc của A lên (R).Tính HI và tính bán kính r

Gọi H là hình chiếu vuông góc của A lên (R). Vì A,

Ta có $A H = d (A, (R)) = \frac{| 2.1 - 2 - 2.1 + 4 |}{\sqrt{2^{2} + {(- 1)}^{2} + {(- 2)}^{2}}} = \frac{2}{3}$

Mà $A H ⊥ (R) \Rightarrow A H ⊥ H I$ ,do đó $Δ A H I$ vuông tại H nên

$H I = \sqrt{A I^{2} - A H^{2}} = \sqrt{2^{2} - {(\frac{2}{3})}^{2}} = \frac{4 \sqrt{2}}{3}$

Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính $r = \frac{4 \sqrt{2}}{3}$

Câu 3

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 36$

B. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 36$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 6$

{(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng $(α)$ có phương trình 2x−2y−z+3=0. Bán kính của (S) là:

A.2

B. $\frac{2}{3}$

C. $\frac{2}{9}$

\frac{4}{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 8 x + 2 y + 2 z - 3 = 0$ và đường thẳng $Δ : \frac{x - 1}{3} = \frac{y}{- 2} = \frac{z + 2}{- 1}$ . Mặt phẳng $(α)$ vuông góc với Δ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình $(α)$ là:

A. $3 x - 2 y - z - 5 = 0$

B. $3 x - 2 y - z + 5 = 0$

C. $3 x - 2 y - z + 15 = 0$

3 x - 2 y - z - 15 = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Mặt phẳng (Oyz) cắt mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 2 y + 4 z - 3 = 0$ theo một đường tròn có tọa độ tâm là

A.(−1;0;0)

B.(0;−1;2)

C.(0;2;−4)

D.(0;1;−2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong không gian Oxyz, cho mặt cầu (C):(x+1)2+(y−3)2+(z−2)2=1 và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?

Trong không gian vớ hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;−1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

Trong không gian Oxyz, cho đường thẳng Δ:x−1−2=y2=z−21 và mặt phẳng P:2x−y+z−3=0. Gọi (S) là mặt cầu có tâm I thuộc và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng α có phương trình 2x−2y−z+3=0. Bán kính của (S) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S:x2+y2+z2−8x+2y+2z−3=0 và đường thẳng Δ:x−13=y−2=z+2−1. Mặt phẳng α vuông góc với Δ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình α là:

Mặt phẳng (Oyz) cắt mặt cầu S:x2+y2+z2+2x−2y+4z−3=0 theo một đường tròn có tọa độ tâm là

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian Oxyz, cho mặt cầu $(C) : {(x + 1)}^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 1$ và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng $(α)$ có phương trình 2x−2y−z+3=0. Bán kính của (S) là:

Mặt phẳng (Oyz) cắt mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 2 y + 4 z - 3 = 0$ theo một đường tròn có tọa độ tâm là