10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)

312 người thi tuần này 4.6 1.1 K lượt thi 10 câu hỏi 60 phút

Đề số 1

🔥 Đề thi HOT:

3084 người thi tuần này

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

8.2 K lượt thi 10 câu hỏi

1386 người thi tuần này

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)

26.7 K lượt thi 30 câu hỏi

723 người thi tuần này

10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)

3.7 K lượt thi 10 câu hỏi

551 người thi tuần này

15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)

4.3 K lượt thi 15 câu hỏi

396 người thi tuần này

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

2.2 K lượt thi 10 câu hỏi

369 người thi tuần này

Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)

12.3 K lượt thi 25 câu hỏi

354 người thi tuần này

23 câu Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2)

6.7 K lượt thi 23 câu hỏi

312 người thi tuần này

10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)

1.4 K lượt thi 10 câu hỏi

Nội dung liên quan:

10 Bài tập Xác định và tính góc giữa hai đường thẳng (có lời giải)

468 lượt thi

1 đề

10 Bài tập Nhận biết và chứng minh hai đường thẳng vuông góc (có lời giải)

338 lượt thi

1 đề

10 Bài tập Nhận biết và chứng minh đường thẳng vuông góc với mặt phẳng (có lời giải)

341 lượt thi

1 đề

10 Bài tập Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng (có lời giải)

394 lượt thi

1 đề

10 Bài tập Xác định hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác (có lời giải)

719 lượt thi

1 đề

10 Bài tập Vận dụng định lí ba đường vuông góc để chứng minh hai đường thẳng vuông góc (có lời giải)

443 lượt thi

1 đề

10 Bài tập Xác định và tính góc giữa đường thẳng và mặt phẳng (có lời giải)

415 lượt thi

1 đề

10 Bài tập Xác định và tính góc giữa hai mặt phẳng (có lời giải)

335 lượt thi

1 đề

10 Bài tập Nhận biết và chứng minh hai mặt phẳng vuông góc (có lời giải)

321 lượt thi

1 đề

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

1823 lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Một hồ bơi hình hộp chữ nhật có đáy là hình vuông cạnh bằng 50 m. Lượng nước trong hồ cao 1,5m. Thể tích nước trong hồ là:

A. 3750 m³;

B. 2500 m³;

C. 1250 m³;

D. 1875 m³.

Lời giải

Đáp án đúng là: A

Thể tích nước trong hồ là: V = 1,5.50² = 3750 m³.

Câu 2

Một khối gỗ có dạng là lăng trụ, biết diện tích đáy và chiều cao lần lượt là 0,25 m² và 1,2 m. Mỗi mét khối gỗ này trị giá 5 triệu đồng. Hỏi khối gỗ đó có giá trị bao nhiêu tiền?

A. 750 000 đồng;

B. 500 000 đồng;

C. 1 500 000 đồng;

D. 3 000 000 đồng.

Lời giải

Đáp án đúng là: C

Thể tích khối gỗ là: V = S.h = 0,25.1,2 = 0,3 (m³).

Vậy khối gỗ đó có giá là: 0,3.5 000 000 = 1 500 000 đồng.

Câu 3

Từ một tấm bìa hình vuông người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 6 cm, rồi gập tấm bìa lại để được một chiếc hộp không nắp có dạng hình hộp chữ nhật. Tính cạnh của tấm bìa ban đầu, biết rằng thể tích của chiếc hộp bằng 600 cm³.

A. 22 cm;

B. 10 cm;

C. 10 dm;

D. 22 dm.

Lời giải

Đáp án đúng là: A

Từ một tấm bìa hình vuông người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, (ảnh 1)

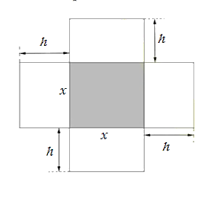
Giả sử tấm bìa ban đầu có cạnh x (cm) (x > 12).

Khi đó đáy của chiếc hộp là hình vuông cạnh x – 12 (cm)

nên diện tích đáy là (x – 12)² (cm²).

Vì thể tích của chiếc hộp bằng 600 cm³ nên

(x – 12)².6 = 600 Þ x – 12 = 10 Þ x = 22. (vì x > 12).

Câu 4

Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt là 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.

A. 76 dm²;

\frac{76}{3}

dm²;

C. 76 dm³;

D .

\frac{76}{3}

dm³.

Lời giải

Đáp án đúng là: D

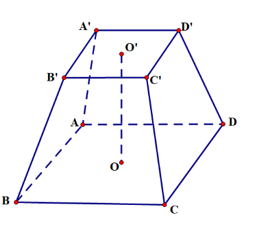
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt là 2 dm và 3 dm, chiều cao bằng 4 dm. (ảnh 1)

Ta có S_ABCD = 3² = 9 dm².

S_A'B'C'D' = 2² = 4 dm².

Thể tích của khối chóp cụt là: $V = \frac{1}{3} .4. (9 + \sqrt{4.9} + 4) = \frac{76}{3}$ dm³.

Câu 5

Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó.

A. 1350 cm²;

B. $\frac{1350}{2} c m^{2}$

C. 1350 cm³;

D. $\frac{1350}{2} c m^{3}$

Lời giải

Đáp án đúng là: C

Thể tích của chiếc bánh chưng đó là V = 15.15.6 = 1350 cm³.

Câu 6

Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3g/cm³.

A. 2160 g;

B. 2106 g;

C. 720 g;

D. 702g.

Lời giải

Đáp án đúng là: A

Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. (ảnh 1)

Diện tích đáy của khối lăng trụ là $S = \frac{1}{2} .12.12 = 72$ (cm²).

Thể tích của khối lăng trụ là: V = S.h = 72.10 = 720 (cm³).

Khối lượng của miếng pho mát đó là: 720.3 = 2160 g.

Câu 7

Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài, chiều rộng và chiều cao của khối hộp đó là 5 m, 1m, 2m. Biết mỗi viên gạch có chiều dài 20 cm, chiều rộng 10 cm, chiều cao 5 cm. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây bồn đó và thể tích thực của bồn chứa là bao nhiêu? (giả sử lượng xi măng và cát không đáng kể).

A. 1180 viên, 8820 lít;

B. 1182 viên, 8800 lít;

C. 1180 viên, 8800 lít;

D. 1182 viên, 8820 lít.

Lời giải

Đáp án đúng là: A

Đổi 20 cm = 0,2 m, 10 cm = 0,1 m, 5 cm = 0,05 m.

Thể tích bồn chứa (gồm cả phần xây gạch) là V₁ = 5.1.2 = 10 m³.

Thể tích bồn chứa (phần xây gạch) là V₂ = 1.0,1.2 + (5 – 0,1).0,1.2 = 1,18 m³.

Thể tích thực của bồn chứa là V = V₁ – V₂ = 10 – 1,18 = 8,820 m³ = 8820 lít.

Thể tích mỗi viên gạch là 0,2.0,1.0,05 = 0,001 m³.

Suy ra cần số viên gạch là: $\frac{V_{2}}{0, 001} = \frac{1, 18}{0, 001} = 1180$ viên.

Câu 8

Một hộp không nắp được làm từ một mảnh bìa các tông như hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích là 500 cm³. Tính độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

A. x = 5 cm;

B. x = 10 cm;

C. x = 2 cm;

D. x = 3 cm.

Lời giải

Đáp án đúng là: B

Thể tích chiếc hộp là V = x.x.h = x².h = 500 $\Rightarrow h = \frac{500}{x^{2}}$ (1).

Để chiếc hộp làm ra ít tốn bìa các tông nhất khi và chỉ khi diện tích toàn phần của hộp là nhỏ nhất.

Diện tích toàn phần của hộp (không nắp) là S_tp = S_đáy + S_{xung quanh} = x² + 4h.x (2).

Thay (1) vào (2), ta được: $x^{2} + 4 x . \frac{500}{x^{2}} = x^{2} + \frac{2000}{x} = x^{2} + \frac{1000}{x} + \frac{1000}{x} \geq 3 \sqrt[3]{1000^{2}}$ .

Dấu “=” xảy ra khi và chỉ khi

x^{2} = \frac{1000}{x} \Leftrightarrow x = 10

Câu 9

Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình vuông trên một mặt) là 4 cm.

A. 27 cm³;

B. 1728 cm³;

C. 1 cm³;

D. 9 cm³.

Lời giải

Đáp án đúng là: A

Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình vuông trên một mặt) là 4 cm. (ảnh 1)

Chu vi của mỗi ô vuông nhỏ là 4 cm nên độ dài mỗi cạnh nhỏ là 1 cm.

Do đó độ dài cạnh rubic là 3.1 = 3 cm.

Thể tích của khối rubic là 3.3.3 = 27 cm³.

Câu 10

Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều như hình vẽ. Biết cạnh của hình vuông bằng 20 cm, OM = x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.

A. x = 9cm;

B. x = 8cm;

C. x = 6cm;

D. x = 7cm.

Lời giải

Đáp án đúng là: B

Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều như hình vẽ. Biết cạnh của hình vuông bằng 20 cm (ảnh 2)

Giả sử ta dựng được hình chóp đều S.ADCM như hình vẽ.

Ta có OM = x Þ AC = 2x, $A M = x \sqrt{2}$ .

Gọi H là trung điểm của MC.

Suy ra OH là đường trung bình của DACM Þ $O H = \frac{x \sqrt{2}}{2}$ và $M H = \frac{x \sqrt{2}}{2}$

Ta có độ dài đường chéo hình vuông 20 cm là $20 \sqrt{2}$

Dấu “=” xảy ra khi 40 – 4x = x Þ x = 8.

4.6

225 Đánh giá

50%

40%

10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)

🔥 Đề thi HOT:

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)

10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)

15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)

23 câu Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2)

10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)

Nội dung liên quan:

10 Bài tập Xác định và tính góc giữa hai đường thẳng (có lời giải)

10 Bài tập Nhận biết và chứng minh hai đường thẳng vuông góc (có lời giải)

10 Bài tập Nhận biết và chứng minh đường thẳng vuông góc với mặt phẳng (có lời giải)

10 Bài tập Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng (có lời giải)

10 Bài tập Xác định hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác (có lời giải)

10 Bài tập Vận dụng định lí ba đường vuông góc để chứng minh hai đường thẳng vuông góc (có lời giải)

10 Bài tập Xác định và tính góc giữa đường thẳng và mặt phẳng (có lời giải)

10 Bài tập Xác định và tính góc giữa hai mặt phẳng (có lời giải)

10 Bài tập Nhận biết và chứng minh hai mặt phẳng vuông góc (có lời giải)

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

Danh sách câu hỏi:

Một hồ bơi hình hộp chữ nhật có đáy là hình vuông cạnh bằng 50 m. Lượng nước trong hồ cao 1,5m. Thể tích nước trong hồ là:

Một khối gỗ có dạng là lăng trụ, biết diện tích đáy và chiều cao lần lượt là 0,25 m2 và 1,2 m. Mỗi mét khối gỗ này trị giá 5 triệu đồng. Hỏi khối gỗ đó có giá trị bao nhiêu tiền?

Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt là 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.

Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó.

Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3g/cm3.

Một hộp không nắp được làm từ một mảnh bìa các tông như hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích là 500 cm3. Tính độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình vuông trên một mặt) là 4 cm.

Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều như hình vẽ. Biết cạnh của hình vuông bằng 20 cm, OM = x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Một khối gỗ có dạng là lăng trụ, biết diện tích đáy và chiều cao lần lượt là 0,25 m² và 1,2 m. Mỗi mét khối gỗ này trị giá 5 triệu đồng. Hỏi khối gỗ đó có giá trị bao nhiêu tiền?

Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3g/cm³.

Một hộp không nắp được làm từ một mảnh bìa các tông như hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích là 500 cm³. Tính độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.