Câu hỏi:

17/07/2022 2,250

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 3sinx + 4cosx − 1

A. min y = −6; max y = 4

B. min y = −5; max y = 5

C. min y = −3; max y = 4

D. min y = −6; max y = 6

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Các hàm số lượng giác !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Bước 1:

Ta có: y = 3sinx + 4cosx − 1

⇔ y + 1 = 3sinx + 4cosx

⇒(y+1)²= (3sinx + 4cosx)²

Bước 2:

Sử dụng bất đẳng thức Bu – nhi – a Cốp – xki:

(ac + bd)²≤ (a²+ b²)(c²+ d²)

. Với a = 3,c = sinx, b = 4, d = cosx

Khi đó

(3.sinx + 4.cosx)²≤ (3²+ 4²)(sin² x + cos² x)

= (3²+ 4²).1 = 25

⇒ −5 ≤ y + 1 ≤ 5
⇔ −6 ≤ y ≤ 4

Bước 3:

Dấu “=” xảy ra $\Leftrightarrow \frac{\sin x}{3} = \frac{\cos x}{4}$

$\Leftrightarrow \tan x = \frac{3}{4}$

$\Leftrightarrow x = \arctan \frac{3}{4} + k π$

Đáp án cần chọn là: A

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm tập xác định của hàm số $y = \tan (2 x - \frac{π}{4})$

A. D = R\ $\{\frac{π}{8} + \frac{k π}{2}, k \in Z\}$

B. D = R\ $\{\frac{3 π}{8} + \frac{k π}{2}, k \in Z\}$

C. D = R\ $\{\frac{3 π}{8} + k π, k \in Z\}$

D. D = R\

\{\frac{3 π}{4} + \frac{k π}{2}, k \in Z\}

Lời giải

Điều kiện:

$\cos (2 x - \frac{π}{4}) \neq 0$

$\Leftrightarrow 2 x - \frac{π}{4} \neq \frac{π}{2} + k π$

$\Leftrightarrow 2 x \neq \frac{3 π}{4} + k π$

$\Leftrightarrow x \neq \frac{3 π}{8} + \frac{k π}{2}$

Đáp án cần chọn là: B

Câu 2

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?

A. $M + n = \frac{9}{8}$

B. $M + n = \frac{9}{7}$

C. $M + n = \frac{8}{7}$

D. $M + n = \frac{7}{8}$

Lời giải

Trả lời:

Ta có: y = cos 2x + cos x = 2cos²x + cosx – 1

Đặt cosx = t, t∈[−1;1].

Hàm số trở thành y = 2t²+ t − 1. Đây là 1 parabol có bề lõm hướng lên, có hoành độ đỉnh $x = - \frac{b}{2 a} = - \frac{1}{4}$

BBT:

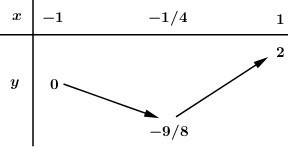
Media VietJack

Dựa vào BBT ta có: $M = 2, m = - \frac{9}{8}$

Vậy $M + m = 2 - \frac{9}{8} = \frac{7}{8}$

Đáp án cần chọn là: D

Câu 3

Hàm số $y = \frac{1 - \sin 2 x}{\cos 3 x - 1}$ xác định trên

A. D = R\ $\{\frac{k 2 π}{3}, k \in Z\}$

B. D = R\ $\{\frac{π}{6} + \frac{k π}{3}, k \in Z\}$

C. D = R\ $\{\frac{k π}{3}, k \in Z\}$

D. D = R\

\{\frac{k π}{2}, k \in Z\}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y = \sqrt{2 \sin x + 3}$

A. $\max y = \sqrt{5}, miny = 1$

B. $\max y = \sqrt{5}, miny = 0$

C. $\max y = \sqrt{5}, miny = \sqrt{3}$

D. $\max y = \sqrt{5}, miny = 3$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin2x+cos22x

y = 2sin² x + cos² 2x:

A. $\max y = 4; \min y = \frac{3}{4}$

B. max y = 3; min y = 2

C. max y = 4; min y = 2

D. $\max y = 3; \min y = \frac{3}{4}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chọn mệnh đề đúng:

A. Hàm số y = sinx có chu kỳ T = π

B. Hàm số y = cosx và hàm số y = tanx có cùng chu kỳ.

C. Hàm số y = cotx và hàm số y = tanx có cùng chu kỳ.

D. Hàm số y = cotx có chu kỳ T = 2π

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 3sinx + 4cosx − 1

Tìm tập xác định của hàm số y=tan2x−π4

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?

Hàm số y=1−sin2xcos3x−1 xác định trên

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=2sinx+3

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin2x+cos22x y = 2sin2 x + cos2 2x:

Chọn mệnh đề đúng:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tìm tập xác định của hàm số $y = \tan (2 x - \frac{π}{4})$

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?

Hàm số $y = \frac{1 - \sin 2 x}{\cos 3 x - 1}$ xác định trên

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y = \sqrt{2 \sin x + 3}$

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin2x+cos22x

y = 2sin² x + cos² 2x: