Câu hỏi:

29/07/2022 182

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x−y−2z+1=0 và ba điểmA(1;−2;0), B(1;0;−1) và C(0;0;−2). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB,AC,BC?

A.4 mặt cầu

B.2 mặt cầu.

C.1 mặt cầu.

D.Vô số mặt cầu

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Mặt cầu và đường thẳng !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có:

$\begin{array}{l} \vec{A B} = (0; 2; - 1) \\ \vec{A C} = (- 1; 2; - 2) \\ [\vec{A B}, \vec{A C}] = (- 2; 1; 2) \end{array}$

Mặt phẳng (ABC) có vecto pháp tuyến là $[\vec{A B}, \vec{A C}] = (- 2; 1; 2)$

Suy ra $(P) / / (A B C)$

Trên mặt phẳng (ABC) có 4 điểm M,N,P,Q cách đều AB,BC,AC là tâm đường tròn nội tiếp, 3 tâm đường tròn bàng tiếp các góc A,B,C do đó có 4 điểm M′,N′,P′,Q′ trên mặt phẳng (P) là hình chiếu vuông góc của M,N,P,Q trên (P) thỏa mãn tính chất cách đều AB,BC,AC.

Tương ứng có 4 mặt cầu tâm M′,N′,P′,Q′ thỏa mãn yêu cầu bài toán.

Đáp án cần chọn là: A

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng $Δ : \frac{x}{1} = \frac{y + 3}{1} = \frac{z}{2}$ . Biết rằng mặt cầu (S) có bán kính bằng $2 \sqrt{2}$ và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.

A.(1;−2;2),I(5;2;10)

B.I(1;−2;2),I(0;3;0)

C.I(5;2;10),I(0;−3;0)

D.I(1;−2;2),I(−1;2;−2)

Lời giải

Tâm I thuộc đường thẳng d nên $I (t; - 3 + t; 2 t)$

Phương trình mặt phẳng $(Oxz) : y = 0$

Ta có bán kính mặt cầu $I M = 2 \sqrt{2}$ mặt cầu cắt mặt phẳng (Oxz) theo đường tròn có bán kính $H M = 2$ suy ra $d (I, (O x z)) = I H = \sqrt{I M^{2} - H M^{2}} = \sqrt{8 - 4} = 2$
Ta có $| - 3 + t | = 2 \Leftrightarrow [\begin{matrix} - 3 + t = 2 \\ - 3 + t = - 2 \end{matrix} \Leftrightarrow [\begin{matrix} t = 5 \Rightarrow I (5; 2; 10) \\ t = 1 \Rightarrow I (1; - 2; 2) \end{matrix}$

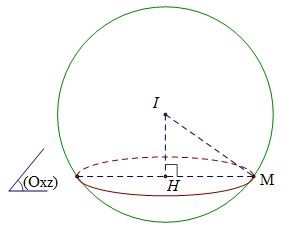
Media VietJack

Đáp án cần chọn là: A

Câu 2

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y - 2}{1} = \frac{z + 1}{2}$ , điểm A(2;−1;1). Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

A. $x^{2} + {(y - 3)}^{2} + {(z - 1)}^{2} = 20$

B. $x^{2} + {(y + 1)}^{2} + {(z + 2)}^{2} = 5$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z + 3)}^{2} = 20$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 14$

Lời giải

Phương trình mặt phẳng (P) qua A , vuông góc (d) là:

$- 1. (x - 2) + 1. (y + 1) + 2. (z - 1) = 0 \Leftrightarrow - x + y + 2 z + 1 = 0$

Gọi $I (1 - t; 2 + t; - 1 + 2 t) = d \cap (P)$ khi đó:

$- (1 - t) + (2 + t) + 2 (- 1 + 2 t) + 1 = 0 \Leftrightarrow t = 0 \Rightarrow I (1; 2; - 1)$

Có $I A^{2} = 14$ . Phương trình mặt cầu là:

${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 14$

Đáp án cần chọn là: D

Câu 3

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$ . Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz.

A. ${(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

C. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 4$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng $(P) : 2 x + 2 y - z - 3 = 0$ và mặt cầu $(S) : {(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 36$ . Gọi $Δ$ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của $Δ$ là:

A. $\{\begin{matrix} x = 2 + 9 t \\ y = 1 + 9 t \\ z = 3 + 8 t \end{matrix}$

B. $\{\begin{matrix} x = 2 - 5 t \\ y = 1 + 3 t \\ z = 3 \end{matrix}$

C. $\{\begin{matrix} x = 2 + t \\ y = 1 - t \\ z = 3 \end{matrix}$

D. $\{\begin{matrix} x = 2 + 4 t \\ y = 1 + 3 t \\ z = 3 - 3 t \end{matrix}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$ là:

A. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 2$

B. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 24$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 50$ .Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.

A. $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$

B.Trục Ox

C.Trục Oy

D.Trục Oz

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d : \{\begin{matrix} x = 2 t \\ y = t \\ z = 4 \end{matrix}$ và $d' : \{\begin{matrix} x = t' \\ y = 3 - t' \\ z = 0 \end{matrix}$ . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d′ là:

A. ${(x - 2)}^{2} + y^{2} + z^{2} = 4$

B. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 2$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 2)}^{2} + {(y + 1)}^{2} + z^{2} = 4$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x−y−2z+1=0 và ba điểmA(1;−2;0), B(1;0;−1) và C(0;0;−2). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB,AC,BC?

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng Δ:x1=y+31=z2 . Biết rằng mặt cầu (S) có bán kính bằng 22 và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:x−1−1=y−21=z+12, điểm A(2;−1;1). Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x+12+y−12+z−22=4. Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz.

Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng P:2x+2y−z−3=0 và mặt cầu S:x−32+y−22+z−52=36. Gọi Δ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của Δ là:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng d:x−11=y2=z−21 là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x−12+y+22+z−32=50.Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d:x=2ty=tz=4 và d':x=t'y=3−t'z=0 . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d′ là:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y - 2}{1} = \frac{z + 1}{2}$ , điểm A(2;−1;1). Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$ . Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz.

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$ là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 50$ .Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.