Câu hỏi:

29/07/2022 1,078

Cho điểm A(0;8;2) và mặt cầu (S) có phương trình $(S) : {(x - 5)}^{2} + {(y + 3)}^{2} + {(z - 7)}^{2} = 72$ và điểm B(1;1;−9). Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử $\vec{n} = (1; m; n)$ là véctơ pháp tuyến của (P). Lúc đó:

A. $m n = \frac{276}{49}$

B. $m n = - \frac{276}{49}$

C. $m n = 4$

m n = - 4

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Mặt cầu và mặt phẳng !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

(S) có tâm I(5;−3;7) và bán kính $R = 6 \sqrt{2}$

Theo đề bài ta có phương trình (P) có dạng $x + m (y - 8) + n (z - 2) = 0$

Vì (P) tiếp xúc với (S) nên

$d (I, (P)) = \frac{|5 + m (- 3 - 8) + n (7 - 2)|}{\sqrt{1 + m^{2} + n^{2}}} = \frac{|5 - 11 m + 5 n|}{\sqrt{1 + m^{2} + n^{2}}} = 6 \sqrt{2}$

$\begin{array}{l} \Leftrightarrow |5 - 11 m + 5 n| = 6 \sqrt{2} . \sqrt{1 + m^{2} + n^{2}} \\ \Leftrightarrow 25 + 121 m^{2} + 25 n^{2} - 110 m + 50 n - 110 m n = 72 (1 + m^{2} + n^{2}) \\ \Leftrightarrow 49 m^{2} - 110 m + 50 n - 110 m n - 47 n^{2} - 47 = 0 \\ \Leftrightarrow 49 m^{2} - 110 m (n + 1) - 47 n^{2} + 50 n - 47 = 0 (1) \\ = 3025 {(n + 1)}^{2} - 49 (- 47 n^{2} + 50 n - 47) = 5328 n^{2} + 3600 n + 5328 > 0 \end{array}$

Phương trình (*) luôn có nghiệm

$\begin{array}{l} d (B, (P)) = \frac{|1 + m (1 - 8) + n (- 9 - 2)|}{\sqrt{1 + m^{2} + n^{2}}} = \frac{|1 - 7 m - 11 n|}{\sqrt{1 + m^{2} + n^{2}}} \\ = > d (B, (P)) \max = A B \Leftrightarrow \frac{|1 - 7 m - 11 n|}{\sqrt{1 + m^{2} + n^{2}}} = 3 \sqrt{19} \Leftrightarrow \sqrt{1 + m^{2} + n^{2}} = \frac{|1 - 7 m - 11 n|}{3 \sqrt{19}} \end{array}$

Mặt khác $\frac{|5 - 11 m + 5 n|}{6 \sqrt{2}} = \sqrt{1 + m^{2} + n^{2}}$

$\frac{|1 - 7 m - 11 n|}{3 \sqrt{19}} = \frac{|5 - 11 m + 5 n|}{6 \sqrt{2}}$

$\begin{array}{l} 72 (1 + 49 m^{2} + 121 n^{2} - 14 m - 22 n + 154 m n) = 171 (25 + 121 m^{2} + 25 n^{2} - 110 m + 50 n - 110 m n) \\ \Leftrightarrow 8 (1 + 49 m^{2} + 121 n^{2} - 14 m - 22 n + 154 m n) = 19 (25 + 121 m^{2} + 25 n^{2} - 110 m + 50 n - 110 m n) \\ \Leftrightarrow - 1907 m^{2} + 493 n^{2} + 1978 m - 1126 n + 3322 m n - 467 = 0 (2) \end{array}$

Từ (1) và (2) $\Rightarrow m . n = \frac{276}{49}$
Đáp án cần chọn là: A

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, cho mặt cầu $(C) : {(x + 1)}^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 1$ và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?

A. 6

B. 4

C. 2

D. 1

Lời giải

Bước 1:

Dễ dàng nhận thấy O,A,B đều nằm ngoài mặt cầu (C) nên (OAB) không cắt mặt cầu (C).

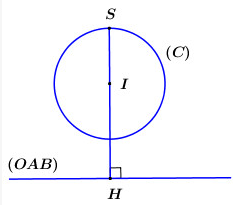
Mặt cầu (C) ta có tâm I(−1;3;2), bán kính R=1.

Ta có $\vec{O A} = (2; 1; 0), \vec{O B} = (0; 2; 0) \Rightarrow [\vec{O A}; \vec{O B}] = (0; 0; 4)$

$\Rightarrow S_{Δ O A B} = \frac{1}{2} |[\vec{O A}; \vec{O B}]| = 2$

Bước 2:

$\Rightarrow V_{S . O A B} = \frac{1}{3} d (S; (O A B)) . S_{Δ O A B}$

Vì $S_{Δ O A B}$ không đổi nên $V_{S . O A B}$ đạt giá trị lớn nhất khi và chỉ khi
$d (S; (O A B))$ lớn nhất, khi đó $d (S; (O A B)) = R + d (I; (O A B))$

Bước 3:

Mặt phẳng (OAB) nhận $\vec{n} = \frac{1}{4} [\vec{O A}; \vec{O B}] = (0; 0; 1)$ là 1 VTPT nên có phương trình: z = 0.

$\Rightarrow d (I; (O A B)) = |z_{I}| = 2 \Rightarrow d {(S; (O A B))}_{\max} = 1 + 2 = 3$

Vậy $\max V_{S . O A B} = \frac{1}{3} .3.2 = 2$

Đáp án cần chọn là: C

Câu 2

Trong không gian vớ hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;−1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. $x + y - 3 z - 8 = 0$

B. $x - y - 3 z + 3 = 0$

C. $x + y + 3 z - 9 = 0$

x + y - 3 z + 3 = 0

Lời giải

(P) là mặt phẳng tiếp xúc với (S) tại A nếu và chỉ nếu (P) đi qua A và $\vec{I A} ⊥ (P)$

Ta có: $\vec{I A} = (- 1; - 1; 3)$ là vec tơ pháp tuyến của mặt phẳng (P).

Mà (P) lại đi qua A(2;1;2) nên: $(P) : - 1 (x - 2) - 1 (y - 1) + 3 (z - 2) = 0 \Leftrightarrow x + y - 3 z + 3 = 0$

Đáp án cần chọn là: D

Câu 3

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 36$

B. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 36$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 6$

{(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : 2 x - y - 2 z - 2 = 0$ và mặt phẳng $(Q) : 2 x - y - 2 z + 10 = 0$ song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó

A. $r = \frac{2 \sqrt{5}}{3}$

B. $r = \frac{4 \sqrt{2}}{3}$

C. $r = \frac{2 \sqrt{2}}{3}$

r = \frac{\sqrt{5}}{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng $(α)$ có phương trình 2x−2y−z+3=0. Bán kính của (S) là:

A.2

B. $\frac{2}{3}$

C. $\frac{2}{9}$

\frac{4}{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 8 x + 2 y + 2 z - 3 = 0$ và đường thẳng $Δ : \frac{x - 1}{3} = \frac{y}{- 2} = \frac{z + 2}{- 1}$ . Mặt phẳng $(α)$ vuông góc với Δ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình $(α)$ là:

A. $3 x - 2 y - z - 5 = 0$

B. $3 x - 2 y - z + 5 = 0$

C. $3 x - 2 y - z + 15 = 0$

3 x - 2 y - z - 15 = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Mặt phẳng (Oyz) cắt mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 2 y + 4 z - 3 = 0$ theo một đường tròn có tọa độ tâm là

A.(−1;0;0)

B.(0;−1;2)

C.(0;2;−4)

D.(0;1;−2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Trong không gian Oxyz, cho mặt cầu $(C) : {(x + 1)}^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 1$ và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng $(α)$ có phương trình 2x−2y−z+3=0. Bán kính của (S) là:

Mặt phẳng (Oyz) cắt mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 2 y + 4 z - 3 = 0$ theo một đường tròn có tọa độ tâm là