Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 600. Thể tích khối chóp S.ABC là: A. a3312 B. a3224 C. a3324 D. a324

Bước 1: Gọi G là trọng tâm tam giác ABC. Vì chóp S.ABC đều nên SG⊥ABC Gọi D là trung điểm của BC ta có: AD⊥BC Ta có: BC⊥ADBC⊥SG(SG⊥(ABC))⇒BC⊥(SAD)⇒BC⊥SD (SBC)∩(ABC)=BC(SBC)⊃SD⊥BC(ABC)⊃AD⊥BC⇒((SBC);(A^BC))=(SD;A^D)=SDA^=600 Bước 2: Vì tam giác ABC đều cạnh a nên AD=a32⇒DG=13AD=a36 SG⊥ABC⇒SG⊥AD⇒ΔSGD vuông tại G ⇒SG=GD.tan60=a36.3=a2 Bước 3: Tam giác ABC đều ⇒SΔABC=a234 Bước 4: ⇒VS.ABC=13SG.SΔABC=13.a2.a234=a3324 Đáp án cần chọn là: C

Câu hỏi:

01/08/2022 1,085

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 60⁰. Thể tích khối chóp S.ABC là:

A. $\frac{a^{3} \sqrt{3}}{12}$

B. $\frac{a^{3} \sqrt{2}}{24}$

C. $\frac{a^{3} \sqrt{3}}{24}$

D. $\frac{a^{3}}{24}$

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Thể tích khối chóp !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Bước 1:

Gọi G là trọng tâm tam giác ABC. Vì chóp S.ABC đều nên $S G ⊥ (A B C)$

Gọi D là trung điểm của BC ta có: $A D ⊥ B C$

Ta có: $\begin{matrix} B C ⊥ A D \\ B C ⊥ S G (S G ⊥ (A B C)) \end{matrix}\} \Rightarrow B C ⊥ (S A D) \Rightarrow B C ⊥ S D$

$\begin{matrix} (S B C) \cap (A B C) = B C \\ (S B C) \supset S D ⊥ B C \\ (A B C) \supset A D ⊥ B C \end{matrix}\} \Rightarrow ((S B \hat{C); (A} B C)) = (S \hat{D; A} D) = \hat{S D A} = 60^{0}$

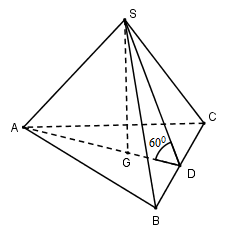
Media VietJack

Bước 2:

Vì tam giác ABC đều cạnh a nên $A D = \frac{a \sqrt{3}}{2} \Rightarrow D G = \frac{1}{3} A D = \frac{a \sqrt{3}}{6}$

$S G ⊥ (A B C) \Rightarrow S G ⊥ A D \Rightarrow Δ S G D$ vuông tại G

$\Rightarrow S G = G D . \tan 60 = \frac{a \sqrt{3}}{6} . \sqrt{3} = \frac{a}{2}$

Bước 3:

Tam giác ABC đều $\Rightarrow S_{Δ A B C} = \frac{a^{2} \sqrt{3}}{4}$

Bước 4:

$\Rightarrow V_{S . A B C} = \frac{1}{3} S G . S_{Δ A B C} = \frac{1}{3} . \frac{a}{2} . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{24}$

Đáp án cần chọn là: C

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp đều S.ABCD có diện tích đáy là $16 c m^{2}$ , diện tích một mặt bên là $8 \sqrt{3} c m^{2}$ . Thể tích khối chóp S.ABCD là:

A. $\frac{32 \sqrt{2}}{3} c m^{3}$

B. $\frac{32 \sqrt{13}}{3} c m^{3}$

C. $\frac{32 \sqrt{11}}{3} c m^{3}$

D. $4 c m^{3}$

Lời giải

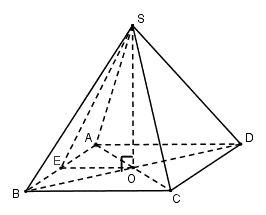
Gọi $O = A C \cap B D$ .Vì chóp S.ABCD đều nên $S O ⊥ (A B C D)$

Vì chóp S.ABCD đều nên ABCD là hình vuông

$\Rightarrow S_{A B C D} = A B^{2} = 16 \Rightarrow A B = 4 (c m) = A D$

Gọi E là trung điểm của AB⇒OE là đường trung bình của tam giác ABD
$\Rightarrow O E / / A D \Rightarrow O E ⊥ A B$ và $O E = \frac{1}{2} A D = \frac{1}{2} .4 = 2 (c m)$

$\begin{matrix} O E ⊥ A B \\ S O ⊥ A B (S O ⊥ (A B C D)) \end{matrix}\} \Rightarrow A B ⊥ (S O E) \Rightarrow A B ⊥ S E$

$\Rightarrow S_{Δ S A B} = \frac{1}{2} S E . A B = 8 \sqrt{3} \Rightarrow S E = \frac{16 \sqrt{3}}{A B} = \frac{16 \sqrt{3}}{4} = 4 \sqrt{3} (c m)$

$S O ⊥ (A B C D) \Rightarrow S O ⊥ O E \Rightarrow Δ S O E$ vuông tại O

$\Rightarrow S O = \sqrt{S E^{2} - O E^{2}} = \sqrt{48 - 4} = \sqrt{44} = 2 \sqrt{11} (c m)$

Vậy $V_{S . A B C D} = \frac{1}{3} S O . S_{A B C D} = \frac{1}{3} .2 \sqrt{11} .16 = \frac{32 \sqrt{11}}{3} (c m^{3})$

Media VietJack

Đáp án cần chọn là: C

Câu 2

Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết $S B = a$ , SC hợp với (SAB) một góc 30⁰ và (SAC) hợp với đáy (ABC) một góc 60⁰. Thể tích khối chóp là:

A. $\frac{a^{3} \sqrt{3}}{27}$

B. $\frac{a^{3} \sqrt{3}}{9}$

C. $\frac{a^{3}}{27}$

D. $\frac{a^{3}}{9}$

Lời giải

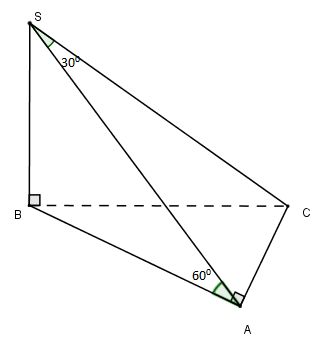
Media VietJack

Ta có:

$\begin{matrix} A C ⊥ A B \\ A C ⊥ S B (S B ⊥ (A B C)) \end{matrix}\} \Rightarrow A C ⊥ (S A B) \Rightarrow A C ⊥ S A$

⇒SA là hình chiếu vuông góc của SC trên

(S A B) \Rightarrow \hat{(S C; (S A B))} = \hat{(S C; S A)} = \hat{C S A} = 30^{0}

\begin{matrix} (S A C) \cap (A B C) = A C \\ (S A C) \supset S A ⊥ A C \\ (A B C) \supset A B ⊥ A C \end{matrix}\} \Rightarrow ((S A \hat{C); (A} B C)) = (S \hat{A; A} B) = \hat{S A B} = 60^{0}

$S B ⊥ (A B C) \Rightarrow S B ⊥ A B \Rightarrow Δ S A B$ vuông tại B

$\Rightarrow A B = S B . \cot 60^{0} = a . \frac{1}{\sqrt{3}} = \frac{a \sqrt{3}}{3}$

$\Rightarrow S A = \sqrt{S B^{2} + A B^{2}} = \sqrt{a^{2} + \frac{a^{2}}{3}} = \frac{2 a}{\sqrt{3}}$

Xét tam giác vuông SAC ta có: $A C = S A . \tan 30^{0} = \frac{2 a}{\sqrt{3}} . \frac{1}{\sqrt{3}} = \frac{2 a}{3}$

S_{A B C} = \frac{1}{2} A B . A C = \frac{1}{2} \frac{a \sqrt{3}}{3} . \frac{2 a}{3} = \frac{a^{2} \sqrt{3}}{9}

V_{S . A B C} = \frac{1}{3} S B . S_{A B C} = \frac{1}{3} . a . \frac{a^{2} \sqrt{3}}{9} = \frac{a^{3} \sqrt{3}}{27}

Đáp án cần chọn là: A

Câu 3

Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn $S A ⊥ (A B C D)$ và $A B = 2 A D = 2 C D = 2 a = \sqrt{2} S A$ . Thể tích khối chóp S.BCD là:

A. $\frac{2 a^{3} \sqrt{2}}{3}$

B. $\frac{a^{3} \sqrt{2}}{6}$

C. $\frac{2 a^{3}}{3}$

D. $\frac{a^{3} \sqrt{2}}{12}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng $a \sqrt{3}$ . Thể tích khối chóp S.ABCD là:

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $4 a^{3} \sqrt{3}$

C. $a^{3} \sqrt{3}$

D. $\frac{4 a^{3} \sqrt{3}}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 2, $∠ B A D = 60^{0}, S A = S C$ và tam giác SBD vuông cân tại S. Gọi E là trung điểm của SC. Mặt phẳng (P) qua AE và cắt hai cạnh SB,SD lần lượt tại M và N. Thể tích lớn nhất $V_{0}$ của khối đa diện ABCDNEM bằng:

A. $V_{0} = \frac{2 \sqrt{3}}{9}$

B. $V_{0} = \frac{8 \sqrt{3}}{21}$

C. $V_{0} = \frac{2 \sqrt{3}}{7}$

D. $V_{0} = \frac{4 \sqrt{3}}{9}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và $S A = a$ . Điểm M thuộc cạnh SA sao cho $\frac{S M}{S A} = k$ . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

A. $k = \frac{- 1 + \sqrt{3}}{2}$

B. $k = \frac{- 1 + \sqrt{5}}{2}$

C. $k = \frac{- 1 + \sqrt{2}}{2}$

D. $k = \frac{1 + \sqrt{5}}{4}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình chóp S.ABC có $A B = A C = 4, B C = 2, S A = 4 \sqrt{3}, \hat{S A B} = \hat{S A C} = 30^{0}$ . Tính thể tích khối chóp S.ABC.

A. $V_{S . A B C} = 8$

B. $V_{S . A B C} = 6$

C. $V_{S . A B C} = 4$

D. $V_{S . A B C} = 12$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 60⁰. Thể tích khối chóp S.ABC là:

Cho hình chóp đều S.ABCD có diện tích đáy là $16 c m^{2}$ , diện tích một mặt bên là $8 \sqrt{3} c m^{2}$ . Thể tích khối chóp S.ABCD là:

Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết $S B = a$ , SC hợp với (SAB) một góc 30⁰ và (SAC) hợp với đáy (ABC) một góc 60⁰. Thể tích khối chóp là:

Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn $S A ⊥ (A B C D)$ và $A B = 2 A D = 2 C D = 2 a = \sqrt{2} S A$ . Thể tích khối chóp S.BCD là:

Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng $a \sqrt{3}$ . Thể tích khối chóp S.ABCD là:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và $S A = a$ . Điểm M thuộc cạnh SA sao cho $\frac{S M}{S A} = k$ . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

Cho hình chóp S.ABC có $A B = A C = 4, B C = 2, S A = 4 \sqrt{3}, \hat{S A B} = \hat{S A C} = 30^{0}$ . Tính thể tích khối chóp S.ABC.