10 Bài tập Nhận biết và chứng minh hai mặt phẳng vuông góc (có lời giải)
44 người thi tuần này 4.6 641 lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: A
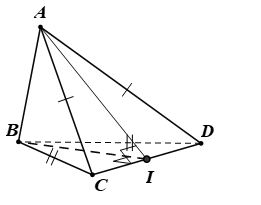
Tam giác BCD cân tại B có I là trung điểm đáy CD ⇒ CD ^ BI (1).
Tam giác ACD cân tại A có I là trung điểm đáy CD ⇒ CD ^ AI (2).
Do đó góc giữa hai mặt phẳng (ACD) và (BCD) là . Suy ra đáp án B đúng.
(1) và (2) ⇒ CD ^ (ABI).
Mà CD Ì (BCD) ⇒ (BCD) ^ (ABI). Suy ra đáp án C đúng.
CD Ì (ACD) ⇒ (ACD) ^ (ABI). Suy ra đáp án D đúng.
Câu 2
Lời giải
Đáp án đúng là: D
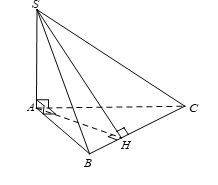
Vì SA ^ (ABC) mà SA Ì (SAB) ⇒ (SAB) ^ (ABC). Do đó đáp án A đúng.
Vì SA ^ (ABC) nên SA ^ AB mà AB ^ AC suy ra AB ^ (SAC).
Lại có AB Ì (SAB) nên (SAB) ^ (SAC). Do đó đáp án B đúng.
Có AH ^ BC và BC ^ SA (do SA ^ (ABC)) do đó BC ^ (SAH) ⇒ BC ^ SH.
Do đó góc giữa hai mặt phẳng (SBC) và (ABC) bằng . Do đó đáp án C đúng.
Vậy đáp án D sai.
Câu 3
Lời giải
Đáp án đúng là: C
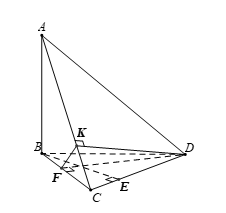
Vì AB ^ (BCD) nên AB ^ CD mà BE ^ CD suy ra CD ^ (ABE).
Lại có CD Ì (ADC) nên (ADC) ^ (ABE). Do đó đáp án A đúng.
Vì AB ^ (BCD) nên AB ^ DF mà DF ^ BC suy ra DF ^ (ABC) ⇒ DF ^ AC.
Lại có DK ^ AC nên AC ^ (DFK).
Mặt khác AC Ì (ADC) suy ra (ADC) ^ (DFK). Do đó đáp án B đúng.
Vì CD ^ (ABE) mà CD Ì (BCD) suy ra (BDC) ^ (ABE). Do đó đáp án D đúng.
Vậy đáp án C sai.
Câu 4
Lời giải
Đáp án đúng là: D
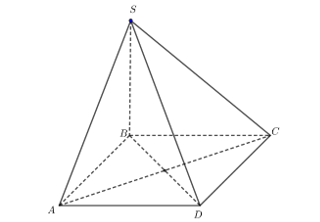
Vì ABCD là hình thoi nên AC ^ BD.
Do SB ^ (ABCD) ⇒ SB ^ AC mà AC ^ BD nên AC ^ (SBD).
Lại có AC Ì (SAC) ⇒ (SAC) ^ (SBD).
Câu 5
Lời giải
Đáp án đúng là: A
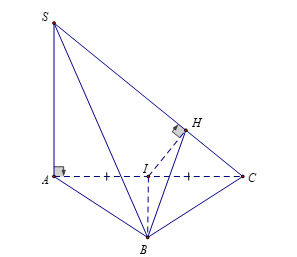
Vì DABC cân tại B, BI là đường trung tuyến nên BI đồng thời là đường cao.
Suy ra BI ^ AC.
Mà SA ^ (ABC) ⇒ SA ^ BI mà BI ^ AC nên BI ^ (SAC) ⇒ BI ^ SC (1).
Lại có IH ^ SC (2).
Từ (1) và (2, suy ra SC ^ (BIH) mà SC Ì (SBC). Do đó (BIH) ^ (SBC).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.