Phần mềm như Google Maps sử dụng công thức Haversine và phương pháp hình học cầu để tính toán khoảng cách giữa hai điểm dựa trên tọa độ địa lý của chúng.

Xuất phát từ việc chuyển đổi tọa độ địa lý sang tọa độ không gian Oxyz, tính góc giữa hai điểm trên bề mặt hình cầu và sau đó chuyển đổi góc đó thành khoảng cách cung tròn.

Câu 2/14

Trong không gian Oxyz, cho mặt cầu (S) tâm I (a; b; c) bán kính R (H.5.41). Khi đó, một điểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện gì?

Lời giải

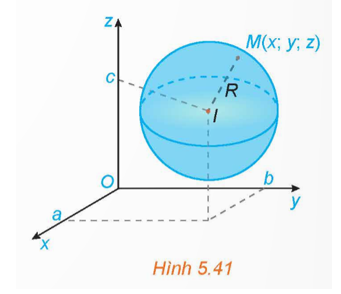
Điểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi IM = R

Û $\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R$ hay (x – a)² + (y − b)² + (z – c)² = R².

Câu 3/14

Trong không gian Oxyz, cho mặt cầu (S) có phương trình ${(x + 2)}^{2} + y^{2} + {(z + \frac{1}{2})}^{2} = \frac{9}{4}$ .

a) Xác định tâm và bán kính của (S).

b) Hỏi điểm M(2; 0; 1) nằm trong, nằm ngoài hay thuộc mặt cầu (S).

Lời giải

a) Mặt cầu (S) có tâm $I\left( { - 2;0; - \frac{1}{2}} \right)$ và $R = \frac{3}{2}$.

b) Có $IM = \sqrt {{4^2} + {0^2} + {{\left( {\frac{3}{2}} \right)}^2}} = \frac{{\sqrt {73} }}{2} > R$.

Do đó điểm M nằm ngoài mặt cầu.

Câu 4/14

Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:

a) Tâm là gốc tọa độ, bán kính R = 1.

b) Đường kính AB, với A(1; −1; 2), B(2; −3; −1).

Lời giải

a) Mặt cầu (S) có tâm là gốc tọa độ, bán kính R = 1 có phương trình là:

x² + y² + z² = 1.

b) Đoạn thẳng AB có trung điểm $J\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)$.

Mặt cầu (S) có bán kính $R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}$.

Mặt cầu (S) có tâm $J\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)$ và $R = \frac{{\sqrt {14} }}{2}$ có phương trình là:

${\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}$.

Câu 5/14

Trong không gian Oxyz, cho (S) là tập hợp các điểm M(x; y; z) có tọa độ thỏa mãn phương trình (S): x² + y² + z² – 4x + 6y – 12 = 0. Chứng minh rằng (S) là một mặt cầu. Xác định tâm và tính bán kính của mặt cầu đó.

Lời giải

Ta viết phương trình mặt cầu (S) dưới dạng:

x² + y² + z² – 4x + 6y – 12 = 0

Û x² – 4x + 4 + y² + 6y + 9 + z² = 25

Û (x – 2)² + (y + 3)² + z² = 25.

Vậy (S) là mặt cầu có tâm I(2; −3; 0) và R = 5.

Câu 6/14

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} + 4 x - 5 y + 6 z + \frac{25}{4} = 0$ . Xác định tâm, tính bán kính của (S).

Lời giải

Từ phương trình trên ta có a = −2; $b = \frac{5}{2}$; c = −3 và $d = \frac{{25}}{4}$.

Phương trình mặt cầu (S) có tâm $I\left( { - 2;\frac{5}{2}; - 3} \right)$, $R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} .$

Câu 7/14