Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?
Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?
A.36m
B.62m
C.60m
Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Tư duy Toán học - Giới hạn của dãy số !!
Quảng cáo
Trả lời:

Ta coi độ cao nảy lên lần thứ nhất là
=> Đây là cấp số nhân lùi vô hạn với
Khi đó tổng quãng đường quả bóng đã di chuyển là
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 333 viên gạch
B. 334 viên gạch
C. 332 viên gạch
Lời giải
Bước 1: Gọi S1 là diện tích mặt đáy tháp. Biểu diễn diện tích mặt đáy tầng thứ n.
Gọi S1 là diện tích mặt đáy tháp. Ta có:
Theo yêu cầu khi xây dựng tòa tháp, diên tích mặt đáy các tầng tiếp theo là:
….
Bước 2: Tính tổng diện tích mặt sàn 11 tầng.
Tổng diện tích mặt sàn 11 tầng tháp là
Bước 3: Tìm số viên gạch
Diện tích mỗi viên gạch là
Số lượng gạch hoa cần mua là
Vậy cần mua 334 viên gạch
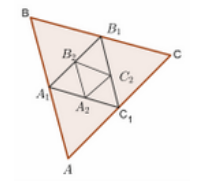
Lời giải
Bước 1:
Gọi là cạnh của tam giác với n nguyên dương.
Ta cần chứng minh cạnh của tam giác bất kì bằng với mọi số nguyên dương n (*)
Vì là trung điểm các cạnh của tam giác ABC nên
Cạnh của tam giác có cạnh là
Giả sử (*) đúng với
Tức là cạnh của tam giác là
Ta có có cạnh bằng một nửa cạnh của tam giác nên có cạnh là
=> (*) đúng với
=> (*) đúng với mọi số nguyên dương n.
=> Chu vi của tam giác như giả thiết là
Bước 2:
Như vậy
Dãy số gồm là cấp số nhân với số hạng đầu là công bội
Đáp án cần chọn là: B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.