8 câu Trắc nghiệm Toán 10 chân trời sáng tạo Tập hợp có đáp án (Thông hiểu)

Hướng dẫn giải

Đáp án đúng là: D

Phương án A đúng vì tập rỗng là tập con của mọi tập hợp.

Phương án B đúng vì 1 là phần tử của A nên ta kí hiệu là 1 ∈ A.

Phương án C đúng vì {1; 2} là một tập hợp, các phần tử của tập hợp này đều thuộc tập hợp A nên tập hợp {1; 2} là tập con của tập hợp A, khi đó ta kí hiệu {1; 2} ⊂ A.

Phương án D sai kí hiệu. Sửa lại: 2 ∈ A.

Vậy ta chọn phương án D.

Hướng dẫn giải

Đáp án đúng là: D

Ta có:

⦁ F ⊂ G nên phương án A sai.

⦁ G ⊂ K nên phương án B sai.

⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.

Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.

Do đó phương án C không đúng trong mọi trường hợp.

⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.

Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:

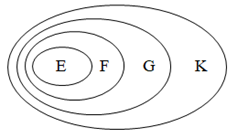
Quan sát biểu đồ Ven, ta thấy E ⊂ K.

Do đó phương án D đúng.

Vậy ta chọn phương án D.

Hướng dẫn giải

Đáp án đúng là: A

⦁ Ta thấy 3 thuộc tập hợp A, ta kí hiệu là 3 ∈ A.

Do đó mệnh đề (I) đúng.

⦁ Vì kí hiệu “{3; 4}” là kí hiệu tập hợp nên mệnh đề (II) sai.

Do phần tử 3 và 4 đều thuộc tập hợp A nên ta có thể sửa lại kí hiệu là: {3; 4} ⊂ H.

⦁ Giải thích tương tự như mệnh đề (II), ta có mệnh đề (III) sai.

Vậy chỉ có mệnh đề (I) đúng.

Do đó ta chọn phương án A.

Hướng dẫn giải

Đáp án đúng là: B

⦁ Ta sử dụng kí hiệu “∈” để biểu diễn một phần tử thuộc tập hợp.

Vì kí hiệu “a” là kí hiệu của phần tử, kí hiệu [a; b] là kí hiệu của tập hợp nên để biểu diễn a là phần tử thuộc tập hợp [a; b], ta kí hiệu là a ∈ [a; b].

Do đó kí hiệu ở phương án A sai.

⦁ Ta sử dụng kí hiệu “⊂” để biểu diễn một tập hợp là tập con của một tập hợp khác.

Vì kí hiệu {a} và [a; b] đều là kí hiệu của tập hợp và phần tử a thuộc tập hợp [a; b] nên ta kí hiệu là {a} ⊂ [a; b].

Do đó kí hiệu ở phương án B đúng.

⦁ Giải thích tương tự như phương án B, ta thu được phương án C sai.

Sửa lại: {a} ⊂ [a; b].

⦁ Vì phần tử a không thuộc tập hợp (a; b] nên kí hiệu ở phương án D sai.

Sửa lại: a ∉ (a; b].

Vậy ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: B

Tập A là tập con của tập B khi mọi phần tử của tập hợp A đều thuộc tập hợp B.

Ta thấy tập hợp A gồm 3 phần tử là: x; y; z.

Tập hợp B gồm 5 phần tử là: x; y; z; t; u.

Trong 4 phương án A, B, C, D, ta thấy tập X ở phương án A và B đều chứa cả 3 phần tử x; y; z, còn phương án C, D không chứa cả 3 phần tử x; y; z.

Nên ta loại phương án C, D.

Ta thấy tập X ở phương án A có phần tử v ∉ B.

Do đó tập X ở phương án A không phải tập con của tập B.

Ta thấy tập X ở phương án B có 4 phần tử là x; y; z; t đều thuộc tập B.

Do đó tập X ở phương án B là tập con của tập hợp B.

Vậy ta chọn đáp án B.