Giải SBT Toán 8 CTST Bài 3. Hình thang cân có đáp án
39 người thi tuần này 4.6 0.9 K lượt thi 6 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 10 (có đáp án)
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
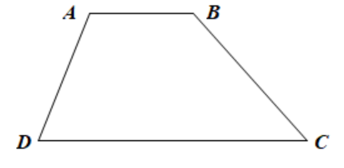
Tứ giác ABCD có tổng 4 góc bằng 360° nên
Mà
Do đó hay .
Suy ra AB // CD.
Vậy tứ giác ABCD là hình thang.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
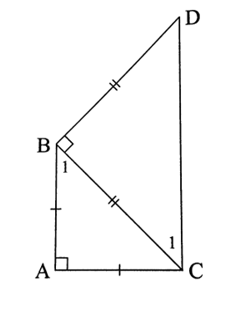
Ta có ∆ABC vuông cân tại A, ∆BCD vuông cân tại B suy ra
Vì và là hai góc ở vị trí so le trong nên AB // CD.
Vậy tứ giác ABDC là hình thang.
Hình thang ABDC có nên ABDC là hình thang vuông.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
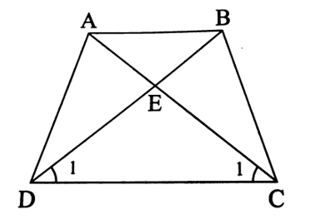
Gọi E là giao điểm của AC và BD.
Trong ∆ECD, ta có nên ∆ECD cân tại E, suy ra EC = ED. (1)
Ta có: AB // CD nên
⦁ (hai góc so le trong);
⦁ (hai góc so le trong);
⦁ (giả thiết).
Suy ra , do đó ∆BEA cân tại E.
Nên AE = BE. (2)
Ta có: AC = AE + EC; BD = BE + ED (3)
Từ (1), (2) và (3) suy ra AC = BD.
Hình thang ABCD có hai đường chéo bằng nhau nên ABCD là hình thang cân.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
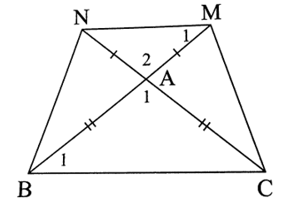
Xét ∆AMN có AM = AN (giả thiết).
Do đó ∆AMN cân tại A, suy ra
Vì ∆ABC cân tại A nên
Lại có (hai góc đối đỉnh) nên
Mà hai góc này ở vị trí so le trong nên MN // BC.
Vậy tứ giác MNBC là hình thang. (1)
Mặt khác, AB = AC; AM = AN.
Suy ra AB + AM = AC + AN, do đó MB = NC (2)
Từ (1) và (2) suy ra MNBC là hình thang cân.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Do BE, CD là hai đường cao nên BE ⊥ AC, CD ⊥ AB.
Xét ∆BEC vuông tại E và ∆CDB vuông tại D, ta có:
BC là cạnh chung; (do ∆ABC cân tại A)
Do đó ∆BEC = ∆CDB (cạnh huyền – góc nhọn)
Suy ra EC = BD (hai cạnh tương ứng)
Mà AC = AB nên AC ‒ EC = AB ‒ BD, hay AE = AD
Do đó ∆ADE cân tại A suy ra (1)
Vì ∆ABC cân tại A nên (2)
Từ (1) và (2) suy ra
Mà hai góc này ở vị trí đồng vị nên DE // BC
Suy ra tứ giác BDEC là hình thang.
Hình thang BDEC có nên là hình thang cân.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập