Giải SGK Toán 12 CTST Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
29 người thi tuần này 4.6 2.5 K lượt thi 24 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
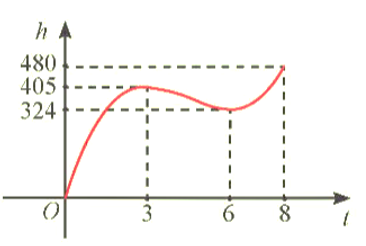
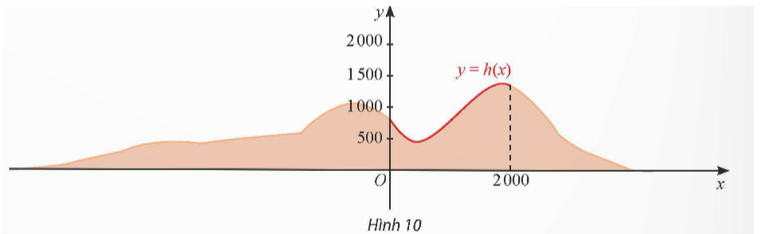
Dựa vào đồ thị ta thấy:
+) Trong khoảng thời gian từ 0 – 3 giây và 6 – 8 giây thì khinh khí cầu tăng dần độ cao.
+) Trong khoảng thời gian từ 3 – 6 giây thì khinh khí cầu giảm dần độ cao.
+) Tại thời điểm 3 phút sau khi xuất phát khinh khí cầu đang ở điểm chuyển từ tăng dần sang giảm dần nên độ cao của nó đang đạt cực đại.
+) Tại thời điểm 6 phút sau khi xuất phát, khinh khí cầu đang ở điểm chuyển từ giảm dần sang tăng dần nên độ cao của nó là một điểm cực tiểu.
Lời giải
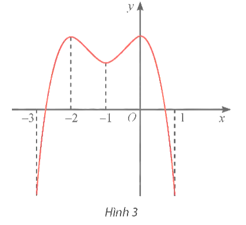
Dựa vào đồ thị hàm số ta có:
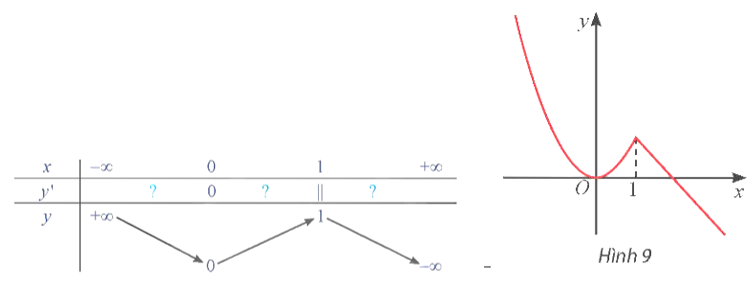
Hàm số đồng biến trên các khoảng (−∞; −2) và (−1; 0).
Hàm số nghịch biến trên các khoảng (−2; −1) và (0; +∞).
Lời giải
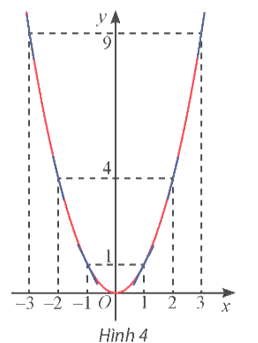
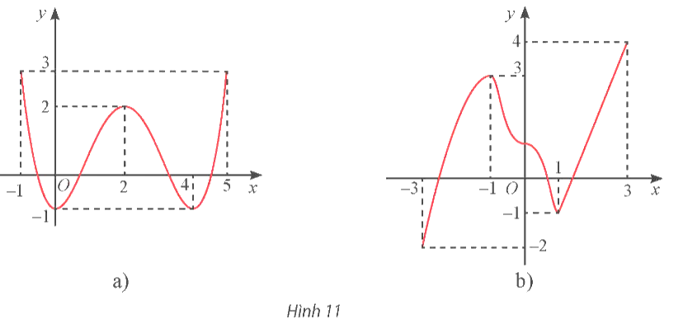
a) Dựa vào đồ thị của hàm số, ta có:
Hàm số đồng biến trên khoảng (0; +∞).
Hàm số nghịch biến khoảng (−∞; 0).
b) f'(x) = 2x; f'(x) = 0 Û x = 0.
Lập bảng biến thiên của hàm số
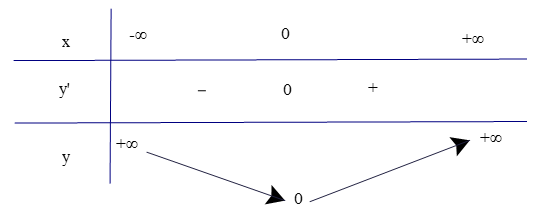
c) Hàm đồng đống biến khi f'(x) > 0 và nghịch biến khi f'(x) < 0.
Lời giải
a) Tập xác định: D = ℝ.
Ta có f'(x) = 3x2 – 12x + 9; f'(x) = 0 Û 3x2 – 12x + 9 = 0 Û x = 1 hoặc x = 3.
Bảng biến thiên:
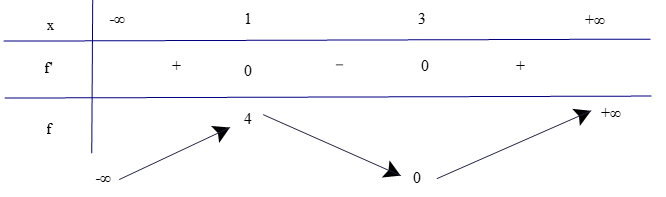
Vậy hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞), nghịch biến trên khoảng (1; 3).
Lời giải
Ta có
Bảng biến thiên
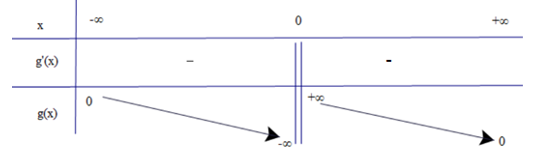
Vậy hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.