Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Có 6 con vật trong hình vẽ, bao gồm: con voi, con khỉ, con ngựa, con chó, con mèo, con chuột.
Do đó câu trả lời của bạn An là sai, câu trả lời của bạn Khoa là đúng.
Sau bài học này ta sẽ được biết những phát biểu xét được tính đúng sai như phát biểu của bạn An và bạn Khoa là một mệnh đề.
Lời giải
Trong hình vẽ đã cho có tất cả 6 con vật, khi đó:
a) Câu “ Có 6 con vật xuất hiện trong hình vẽ” là đúng.
b) Câu “ Có 5 con vật xuất hiện trong hình vẽ” là sai.
c) Câu “ Có bao nhiêu con vật xuất hiện trong hình vẽ?” là câu hỏi. Do đó câu này không xác định được tính đúng sai.
Lời giải
+) “13 là số nguyên tố” là một mệnh đề và là một mệnh đề đúng.
+) Theo bất đẳng thức tam giác tổng độ dài của hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại. Do đó “Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại” là một mệnh đề sai.
+) “Bạn đã làm bài tập chưa?” là một câu hỏi không xác định được tính đúng sai. Do đó đây không phải một mệnh đề.
+) “Thời tiết hôm nay thật đẹp!” là một câu cảm thán về thời tiết, không phải một câu khẳng định có tính đúng sai. Do đó đây không phải mệnh đề.
Khi đó, ta có bảng:
|
Câu |
Không là mệnh đề |
Mệnh đề đúng |
Mệnh đề sai |
|
13 là số nguyên tố. |
|
ü
|
|
|
Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại. |
|
|
ü
|
|
Bạn đã làm bài tập chưa? |
ü
|
|
|
|
Thời tiết hôm nay thật đẹp! |
ü
|
|
|
Lời giải
+) Với x = 4 ta có mệnh đề “4 > 5” là một mệnh đề sai.
+) Với x = 7 ta có mệnh đề “7 > 5” là một mệnh đề đúng.Lời giải
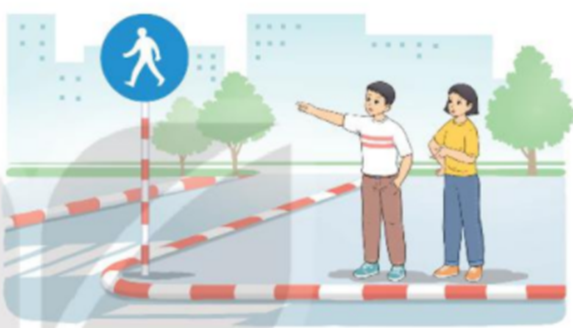
Phát biểu ý kiến của An dưới dạng một mệnh đề như sau:
“Đây không phải là biển báo đường dành cho người đi bộ”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.