Giải SGK Toán 11 CD Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện có đáp án

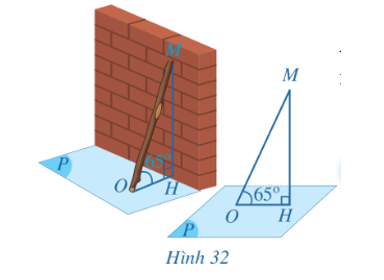
Góc nghiêng giữa chiếc gậy và mặt đất được hiểu là góc tạo bởi giữa chiếc gậy và đường thẳng hình chiếu của chiếc gậy đó xuống mặt đất.

a) Vì MH ⊥ (P) và O ∈ (P) nên hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng HO.

b) Vì hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng HO nên góc giữa đường thẳng MO và hình chiếu của đường thẳng đó trên mặt phẳng (P) là góc giữa hai đường thẳng MO và HO và là góc $\widehat{MOH}.$

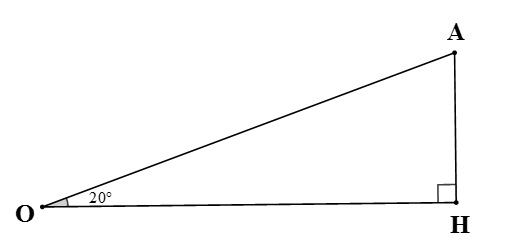
Đổi 200 km/h = $\frac{500}{9}$ m/s.

Bài toán được mô hình hóa như hình vẽ trên, với OA là quãng đường máy bay bay được sau 2 giây, AH là độ cao của máy bay so với mặt đất khi máy bay rời khỏi mặt đất sau 2 giây, góc $\widehat{AOH}$ là góc giữa đường thẳng được tạo thành khi máy bay cất cánh và mặt đất.

Sau 2 giây máy bay bay được quãng đường là $s=vt=\frac{500}{9}\cdot 2=\frac{1000}{9}$ (m).

Hay $OA=\frac{1000}{9}$ (m).

Xét tam giác OAH vuông tại H có: $\sin \widehat{AOH}=\frac{AH}{OA}$ 

Suy ra $AH=OA\cdot \sin \widehat{AOH}=\frac{1000}{9}\cdot \sin 20°\approx 38,0.$

Vậy độ cao của máy bay so với mặt đất sau khi máy bay rời khỏi mặt đất 2 giây là 38,0 m.

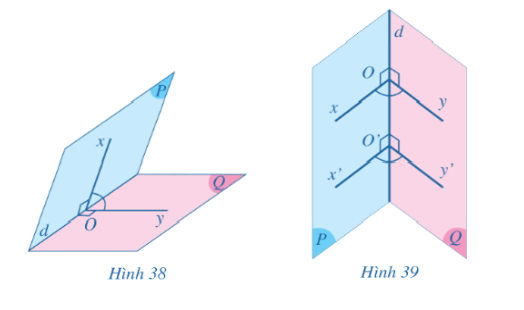
Mỗi trang sổ đều được gắn cố định và giới hạn bởi gáy sổ. Nên nếu mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng thì hai nửa mặt phẳng đó có chung bờ là đường thẳng chứa gáy sổ.

Gọi M, N là hai điểm bất kì lần lượt thuộc hai mặt phẳng (α), (β).

Góc nhị diện được tạo bởi hai mặt phẳng (α), (β) có cạnh của góc nhị diện là đường thẳng d là [M, d, N].

Vì có vô số điểm M và N khác nhau thuộc hai mặt phẳng (α), (β) nên hai mặt phẳng (α), (β) tạo nên vô số góc nhị diện có cạnh của góc nhị diện là đường thẳng d.

Xét (P) có: Ox ⊥ d và Ox’ ⊥ d nên Ox // O’x’.

Xét (Q) có: Oy ⊥ d và Oy’ ⊥ d nên Oy // O’y’.

Từ đó ta có: góc giữa đường thẳng Ox và Oy bằng góc giữa đường thẳng O’x’ và O’y’ hay số đo của hai góc xOy và x’O’y’ bằng nhau.

a) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AD ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AD.

Mà AB ∩ AD = A ∈ SA.

Do đó $\widehat{BAD}$ là góc phẳng nhị diện của góc nhị diện [B, SA, D].

Vì ABCD là hình vuông nên $\widehat{BAD} ={90}^0$

Vậy số đo của góc nhị diện [B, SA, D] bằng 90°.

b) Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC.

Ta có: SA ⊥ AC, SA ⊥ AB (theo câu a) và AC ∩ AB = A ∈ SA.

Do đó $\widehat{BAC}$ là góc phẳng nhị diện của góc nhị diện [B, SA, C].

Vì ABCD là hình vuông nên đường chéo AC là đường phân giác của góc BAD, do đó $\widehat{BAC}=45°.$

Vậy số đo của góc nhị diện [B, SA, C] = 45°.

a) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AC ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AC.

Mà AB ∩ AC = A ∈ SA.

Do đó $\widehat{BAC}$ là góc phẳng nhị diện của góc nhị diện [B, SA, C].

Vì ABCD là hinh thoi cạnh a và AC = a nên ta có AB = AC = BC = a.

Suy ra tam giác ABC đều. Khi đó $\widehat{BAC}=60°.$

Vậy số đo của góc nhị diện [B, SA, C] = 60°.

b) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AD ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AD.

Mà AB ∩ AD = A ∈ SA.

Do đó $\widehat{BAD}$ là góc phẳng nhị diện của góc nhị diện [B, SA, D].

Vì ABCD là hinh thoi cạnh a và AC = a nên ta có AD = AC = CD = a.

Suy ra tam giác ACD đều.

Khi đó $\widehat{CAD}=60°.$

Ta có:$\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=60°+60°=120°.$

Vậy số đo của góc nhị diện [B, SA, D] bằng 120°

c) Vì SA ⊥ (ABCD) nên AC là hình chiếu của SC trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABC) là góc $\widehat{SCA}.$  

Xét tam giác SAC vuông tại (do SA ⊥ AC theo câu a) có:

$\tan \widehat{SCA}=\frac{SA}{AC}=\frac{a}{a}=1.$ Do đó $\widehat{SCA}=45°.$

Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.

a) Ta có SO ⊥ (ABCD) nên OA là hình chiếu của SA trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng $\widehat{SAO}$

Vì tam giác SAC là tam giác đều nên $\widehat{SAO}=60°.$

Vậy số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 60°.

b) Ta có: SO ⊥ (ABCD) và AC ⊂ (ABCD) nên SO ⊥ AC.

Vì ABCD là hình vuông nên AC ⊥ BD.

Ta có: AC ⊥ SO, AC ⊥ BD và SO ∩ BD = O trong (SBD).

Suy ra AC ⊥ (SBD).

Hay AO ⊥ (SBD) nên SO là hình chiếu của SA trên (SBD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (SBD) bằng $\widehat{ASO}$

Do ∆SAC đều nên đường cao SO đồng thời là đường phân giác của góc ASC.

Do đó $\widehat{ASO}=\frac{\widehat{ASC}}{2}=\frac{60°}{2}=30°.$

Vậy góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 30°.

c) Ta có AC ∩ BD = O.

Vì O ∈ BD mà BD ⊂ (SBD) nên O ∈ (SBD).

Suy ra O = AC ∩ (SBD).

Mặt khác AC ⊥ (SBD).

Từ đó ta có O là hình chiếu của A trên (SBD).

Mà S ∈ (SBD) nên ta có SO là hình chiếu của SA trên (SBD).

Như vậy, góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc giữa hai đường thẳng SA và SO và bằng $\widehat{ASO}$

Vì ABCD là hình vuông và AC ∩ BD = O nên O là trung điểm của AC và BD.

Xét tam giác SAC đều có SO là đường trung tuyến (do O là trung điểm của AC).

Suy ra SO cũng là đường phân giác của $\widehat{ASC}.$

Khi đó $\widehat{ASO}=\frac{\widehat{ASC}}{2}=\frac{60°}{2}=30°.$

Vậy số đo của góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 30°.

Bài toán được mô hình hóa như bài vẽ trên, với:

⦁ AB là chiều dài con dốc;

⦁ BI là độ cao của con dốc so với mặt phẳng nằm ngang;

⦁ AH và BK lần lượt là độ cao của điểm A và điểm B so với mặt nước biển.

Theo bài ra ta có: AH = 200 m, BK = 220 m, AB = 120 m và độ dốc của con dốc là góc được tạo bởi đường thẳng AB và đường thẳng AI (do AI là hình chiếu của AB trên mặt phẳng nằm ngang) và chính là số đo của $\widehat{BAI}.$

Dễ thấy AHKI là hình chữ nhật nên IK = AH = 200 m.

Suy ra BI = BK – IK = 220 – 200 = 20 (m).

Vì tam giác ABI vuông tại I nên ta có:

$\sin \widehat{BAI}=\frac{BI}{AB}=\frac{20}{120}=\frac{1}{6}\Rightarrow \widehat{BAI}\approx 9,59°.$

Vì độ dốc 100% tương ứng với góc 90°.

Suy ra góc 9,59° có độ dốc là $\frac{9,59\cdot 100\%}{90}\approx 10,66\%.$

Vậy độ dốc của con dốc đó khoảng 10,66%.