Bài tập: Định lí có đáp án

Thi Online Bài tập: Định lí có đáp án

Đề số 1

Bài tập: Định lí có đáp án

1054 lượt thi
10 câu hỏi
15 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Chứng minh định lý là:

A. Dùng lập luận để từ giả thiết suy ra kết luận

B. Dùng hình vẽ để từ giả thiết suy ra kết luận

C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận

D. Cả A, B, C đều sai

Xem đáp án

Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận

Chọn đáp án A.

Câu 2:

Trong các câu sau, câu nào cho một định lý

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.

C. Nếu hai đường thẳng và cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.

Xem đáp án

Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”

Nên A đúng, B sai

Câu C và D sai vì thiếu từ "phân biệt", hai đường thẳng phân biệt cùng ....

Chọn đáp án A.

Câu 3:

Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là:

A. $a / / b; a ⊥ c$

B. $a / / b; a \cap c = {A}; b \cap c = {B}$

C. $a / / b; a / / c$

D. a // b,c bất kì

Xem đáp án

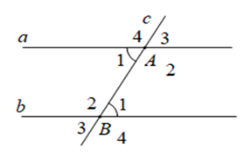
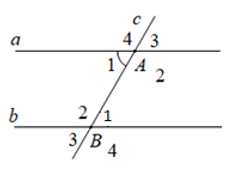
Giả thiết của định lý trên là: a // b, c ∩ a = {A}, c ∩ b = {B}

Chọn đáp án B.

Câu 4:

Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

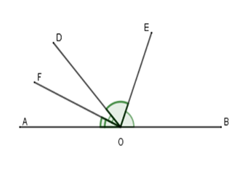
A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF

B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA

C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF

D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OB ⊥ OF

Xem đáp án

Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD.

Kết luận: OE ⊥ OF

Chọn đáp án A.

Câu 5:

Phần giả thiết: $c \cap a = {A}; c \cap b = {B}; \hat{A_{1}} + \hat{B_{2}} = 180^{o}$ (tham khảo hình vẽ) là của định lý nào dưới đây:

A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc ngoài cùng phía bù nhau thì hai đường thẳng đó song song.

B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song.

C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Xem đáp án

Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Chọn đáp án D.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Các bài thi hot trong chương

Đánh giá trung bình

Thi Online Bài tập: Định lí có đáp án