Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án (Đề 6)
18 người thi tuần này 4.6 1.9 K lượt thi 15 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
15 câu Trắc nghiệm Toán 9 Chân trời sáng tạo Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 1
Tổng hợp đề thi giữa học kì 2 Toán 9 hay nhất năm 2023 có đáp án (Đề 1)
Nội dung liên quan:
Danh sách câu hỏi:
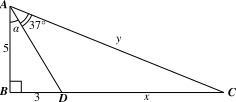
Câu 1
A. \(\left( {x - 1} \right)\left( {x + 1} \right)\).
B. \({\left( {x - 1} \right)^2}\).
C. \({\left( {x + 1} \right)^2}\).
D. \(x\left( {x - 1} \right)\left( {x + 1} \right)\).
Lời giải
Đáp án đúng là: A
Mẫu thức chung của phương trình \[\frac{1}{{x - 1}} + \frac{3}{{x + 1}} = 0\] là \(\left( {x - 1} \right)\left( {x + 1} \right)\).
Câu 2
A. \[S = \left\{ { - 5;\,\,3} \right\}.\]
B. \[S = \left\{ {5;\,\, - 3} \right\}.\]
C. \[S = \left\{ { - 5;\,\, - 3} \right\}.\]
D. \[S = \left\{ {5;\,\,3} \right\}.\]
Lời giải
Giải phương trình:
\[ - 4\left( {x - 5} \right)\left( {9 - 3x} \right) = 0\]
\[\left( {x - 5} \right)\left( {9 - 3x} \right) = 0.\]
\[x - 5 = 0\] hoặc \[9 - 3x = 0\]
\[x = 5\] hoặc \[x = 3.\]
Như vậy, các nghiệm của phương trình đã cho là \[x = 5;\] \[x = 3.\]
Khi đó tập hợp tất cả các nghiệm của phương trình đã cho là \[S = \left\{ {5;\,\,3} \right\}.\]
Vậy ta chọn phương án D.
Câu 3
A. \[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
B. \[5x - 3z = 6\].
C. \(5x - 8y = 0.\)
D. \[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Lời giải
Phương trình bậc nhất hai ẩn có dạng \[ax + by = c\] với \(a \ne 0\) hoặc \(b \ne 0\).
Xét các phương án, ta thấy:
Phương trình \[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\] viết thành \(x + 2y = 11\), đây là phương trình bậc nhất hai ẩn.
Phương trình \[5x - 3z = 6\] là phương trình bậc nhất hai ẩn \(x,z\).
Phương trình \(5x - 8y = 0\) là phương trình bậc nhất hai ẩn \(x,y\)
Phương trình \[\left( {x - 2} \right)\left( {2y - 3} \right) = 3\] viết thành \[2xy - 3x - 4y = - 3\], đây không phải là phương trình bậc nhất hai ẩn.
Ta chọn phương án D.
Câu 4
A. \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{2x + y = 4}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 8}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 7}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{4x - 2y = 0}\\{x + y = - 5}\end{array}} \right.\).
Lời giải
Đáp án đúng là: C
Cách 1. Để kiểm tra xem cặp số \(\left( { - 2;\,\, - 3} \right)\) là nghiệm của hệ phương trình nào, ta thay \(x = - 2\) và \(y = - 3\) vào từng hệ phương trình:
⦁ Xét phương án A. \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{2x + y = 4}\end{array}} \right.\)
Thay\(x = - 2\) và \(y = - 3\) vào hệ phương trình trên ta được: \(\left\{ \begin{array}{l} - 2 - 2 \cdot \left( { - 3} \right) = 4 \ne 3\\2 \cdot \left( { - 2} \right) + \left( { - 3} \right) = - 7 \ne 4.\end{array} \right.\)
Do đó cặp số \(\left( { - 2;\,\, - 3} \right)\) không phải là nghiệm của hệ phương trình ở phương án A.
⦁ Xét phương án B. \(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 8}\end{array}} \right.\)
Thay\(x = - 2\) và \(y = - 3\) vào hệ phương trình trên ta được: \(\left\{ \begin{array}{l}2 \cdot \left( { - 2} \right) - \left( { - 3} \right) = - 1\\ - 2 - 3 \cdot \left( { - 3} \right) = 7 \ne 8.\end{array} \right.\)
Do đó cặp số \(\left( { - 2;\,\, - 3} \right)\) không phải là nghiệm của hệ phương trình ở phương án B.
⦁ Xét phương án C. \(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 7}\end{array}} \right.\)
Thay\(x = - 2\) và \(y = - 3\) vào hệ phương trình trên ta được: \(\left\{ \begin{array}{l}2 \cdot \left( { - 2} \right) - \left( { - 3} \right) = - 1\\ - 2 - 3 \cdot \left( { - 3} \right) = 7.\end{array} \right.\)
Do đó cặp số \(\left( { - 2;\,\, - 3} \right)\) là nghiệm của hệ phương trình ở phương án C.
⦁ Xét phương án D. \(\left\{ {\begin{array}{*{20}{l}}{4x - 2y = 0}\\{x + y = - 5.}\end{array}} \right.\)
Thay\(x = - 2\) và \(y = - 3\) vào hệ phương trình trên ta được: \(\left\{ \begin{array}{l}4 \cdot \left( { - 2} \right) - 2 \cdot \left( { - 3} \right) = - 2 \ne 0\\ - 2 + \left( { - 3} \right) = - 5.\end{array} \right.\)
Do đó cặp số \(\left( { - 2;\,\, - 3} \right)\) không phải là nghiệm của hệ phương trình ở phương án D.
Vậy cặp số \(\left( { - 2;\,\, - 3} \right)\) là nghiệm của hệ phương trình ở phương án C.
Cách 2. Sử dụng máy tính cầm tay để tìm nghiệm của mỗi hệ phương trình.
⦁ Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{2x + y = 4}\end{array}} \right.\). Ta lần lượt bấm các phím

Như vậy, ta thấy rằng cặp số \(\left( { - 2;\,\, - 3} \right)\) không phải là nghiệm của hệ phương trình này.
⦁ Tương tự như trên, ta tìm được \(\left( { - 2;\,\, - 3} \right)\) là nghiệm của hệ phương trình ở phương án C.
Vậy ta chọn phương án C.
Câu 5
A. \(m\) lớn hơn âm 8.
B. \(m\) không nhỏ hơn âm 8.
C. \(m\) nhỏ hơn âm 8.
D. \(m\) không lớn hơn âm 8.
Lời giải
Đáp án đúng là: D
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là \(m\) không lớn hơn âm 8.
Câu 6
A. \(a < b\) và \(c > d\) thì \(a + b < c + d\).
B. \(a < b\) và \(c > d\) thì \(a + c = b + d\).
C. \(a > b\) và \(c > d\) thì \(ac > bd\).
D. \(a > b\) và \(c > d\) thì \(a + c > b + d\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[ - 15x + 4\].
B. \[ - 15x\].
C. \[15x - 4\].
D. \[15x\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(m \ge - 2\).
B. \(m > - 2\).
C. \(m \le - 2\).
D. \(m < - 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(\frac{{MN}}{{NP}}\).
B. \(\frac{{MP}}{{NP}}\).
C. \(\frac{{MN}}{{MP}}\).
D. \(\frac{{MP}}{{MN}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\sin \alpha = \sin \beta \).
B. \(\cos \alpha = \cos \beta \).
C. \(\tan \alpha = \cot \beta \).
D. \(\tan \alpha = \tan \beta \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
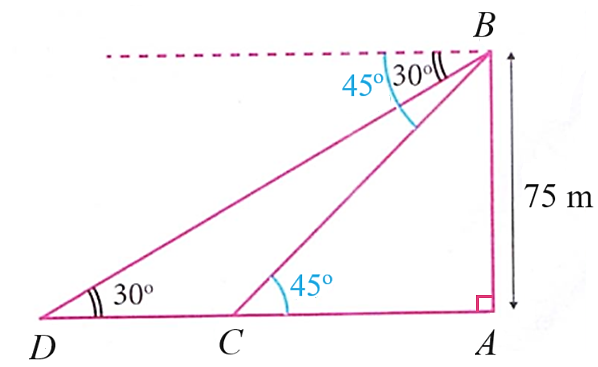
Câu 11
A. \(\widehat B = 60^\circ ;\) \(BC = 20.\)
B. \(\widehat B = 60^\circ ;\) \(BC \approx 8,08.\)
C. \(\widehat B = 60^\circ ;\) \(BC \approx 11,55\).
D. \(\widehat B = 60^\circ ;\) \(BC \approx 14,14.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.