Bài tập Bài 22. Ba đường conic có đáp án

Hướng dẫn giải

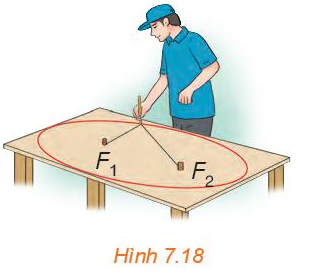
a) Đường vừa nhận được có liên hệ với Hình 7.17b, hai hình này có dạng gần giống nhau.

 b) Trong quá trình đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ đầu bút tới các vị trí F₁, F₂ không thay đổi vì nó luôn bằng độ dài của sợi dây.

Hướng dẫn giải

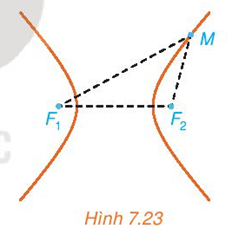
Xét tam giác MF₁F₂, theo bất đẳng thức tam giác ta có: MF₁ + MF₂ > F₁F₂.

Mà MF₁ + MF₂ = 2a, F₁F­₂ = 2c nên 2a > 2c.

Suy ra: a > c.

Hướng dẫn giải

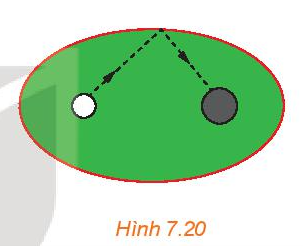
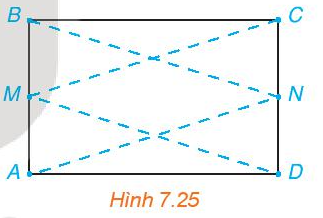
Vị trí ban đầu của bi và vị trí của lỗ thu là 2 tiêu điểm của hình elip, gọi hai tiêu điểm này lần lượt là F₁ và F₂. Bi lăn từ F₁ đến một vị trí M trên hình elip rồi đi đến F₂.

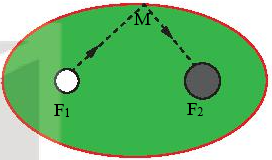
Do đó, quãng đường bi đi được là: MF₁ + MF₂. 

Theo tính chất hình elip thì MF₁ + MF₂ = 2a không đổi.

Vậy độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu không phụ thuộc vào đường đi của bi.

Hướng dẫn giải

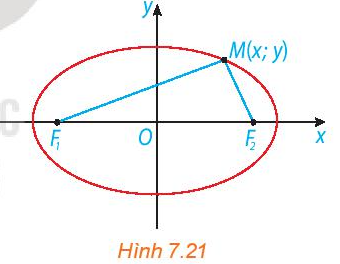
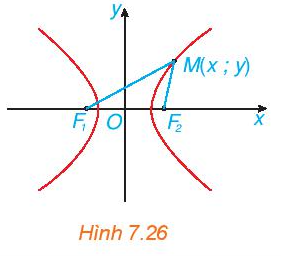
a) Vì F₁F₂ = 2c, mà O là trung điểm của F₁F₂.

Do đó ta có: F₁O = F­₂O = 2c : 2 = c.

Quan sát hình ta thấy, điểm F­₁ thuộc trục Ox, nằm bên trái điểm O và cách O một khoảng bằng F₁O nên tọa độ F_1­(– c; 0).

Điểm F­₂ thuộc trục Ox, nằm bên phải điểm O và cách O một khoảng bằng F₂O nên tọa độ F_2­(c; 0).

Vậy tọa độ các tiêu điểm: F₁(– c; 0) và F₂(c; 0).

b) +) Giả sử M(x; y) thuộc elip (E) ta cần chứng minh: $\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$

Thật vậy, M thuộc elip (E) nên: MF₁ + MF₂ = 2a.

Lại có: MF₁ =$\sqrt{{\left(x-\left(-c\right)\right)}^2+{\left(y-0\right)}^2} = \sqrt{{\left(x+c\right)}^2+y^2}$;

MF₂ = $\sqrt{{\left(x-c\right)}^2+{\left(y-0\right)}^2} = \sqrt{{\left(x-c\right)}^2+y^2}$.

⇒ MF₁ + MF₂  = $\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$

Vậy $\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$.

+) Giả sử $\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$, ta cần chứng minh M thuộc elip (E).

Thật vậy: $\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$ nên: MF₁ + MF₂ = 2a.

Vậy M thuộc elip (E).

Hướng dẫn giải:

Ta có: a² = 100, b² = 64. Do đó c = $\sqrt{a^2-b^2}=\sqrt{100-64}=\sqrt{36}=6$.

Vậy elip có hai tiêu điểm là F₁(– 6; 0); F₂(6; 0) và tiêu cự là F₁F­₂ = 2c = 2 . 6 = 12.

Hướng dẫn giải

Ta có 30 cm trên thực tế ứng với 1 đơn vị trên mặt phẳng tọa độ.

Nên 75 cm trên thực tế ứng với 75 : 30 = 2,5 đơn vị trên mặt phẳng tọa độ.

Gọi điểm M trên elip thỏa mãn có hoành độ là 2,5, suy ra tọa độ M(2,5; y)

Mà M thuộc (E) nên tọa độ điểm M thỏa mãn phương trình (E), do đó:

$\frac{{\left(2,5\right)}^2}{16}+\frac{y^2}{4}=1\Rightarrow y^2=\frac{39}{16}\Rightarrow y=\frac{\sqrt{39}}{4}\approx 1,56$

Khi đó chiều cao của ô thoáng là: h ≈ 1,56 . 30 = 46,8 cm.

Vậy chiều cao của ô thoáng khoảng 46,8 cm.

Hướng dẫn giải

Xét tam giác MF₁F₂, áp dụng bất đẳng thức trong tam giác ta có: |MF₁ – MF₂|  < F₁F₂.

Mà |MF₁ – MF₂| = 2a, F₁F₂ = 2c. Nên 2a < 2a.

Suy ra: a < c.