Bộ 3 đề KSCL đầu năm Toán 9 có đáp án - Đề 3
24 người thi tuần này 4.6 397 lượt thi 5 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
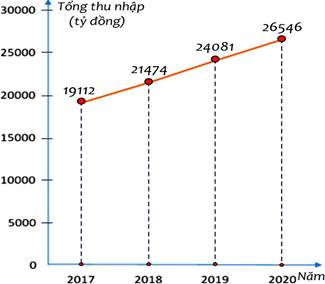
1) a) Ta có bảng thống kê tổng thu nhập của người lao động Việt Nam trong sản xuất thiết bị điện qua các năm như sau:
|
Năm |
2017 |
2018 |
2019 |
2020 |
|
Tổng thu nhập (tỷ đồng) |
\[19\,\,112\] |
\[21\,\,474\] |
\[24\,\,081\] |
\[26\,\,546\] |
b) Tổng thu nhập của người lao động Việt nam trong sản xuất thiết bị điện năm 2017 giảm so với năm 2019 là: \(100\% \cdot \left( {1 - \frac{{19\,\,112}}{{24\,\,081}}} \right) \approx 20,6\% .\)
Vậy nhận định của bài báo là hoàn toàn chính xác.
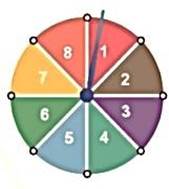
2) a) Biến cố “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 4”.
Các kết quả thuận lợi của biến cố: \[1\,;\,\,2\,;\,\,3.\]
Xác suất của các biến cố là \(\frac{3}{8}.\)
b) Biến cố “Mũi tên chỉ vào hình quạt ghi số nguyên tố”.
Các kết quả thuận lợi của biến cố: \[2\,;\,\,3\,;\,\,5\,;\,\,7.\]
Xác suất của các biến cố là: \(\frac{4}{8} = \frac{1}{2}.\)
Lời giải
|
a) \[{\left( {x + 5} \right)^2} - 3\left( {x + 5} \right) = 0.\] \[\left( {x + 5} \right)\left( {x + 5 - 3} \right)\; = 0\] \[\left( {x + 5} \right)\left( {x + 2} \right)\; = 0\] \[x + 5\; = 0\] hoặc \[x + 2\; = 0\] \[x = - 5\] hoặc \[x = - 2.\] Vậy phương trình đã cho có nghiệm là \[x = - 5\] và \[x = - 2.\] c) \[\left\{ \begin{array}{l}7x + 4y = 10\\4x + y = 7\end{array} \right..\] Từ phương trình thứ hai ta có \[y = 7 - 4x\]. Thế vào phương trình thứ nhất, ta được: \[7x + 4\left( {7 - 4x} \right) = 10\] \[7x + 28 - 16x = 10\] \[16x - 7x = 28 - 10\] \[9x = 18\] \[x = 2\]. Từ đó, ta có \(y = - 1.\) Vậy hệ phương trình đã cho có nghiệm là \[\left( {2\,;\,\,1} \right).\] |
b) \(\frac{{x + 3}}{{x - 3}} - \frac{8}{x} = \frac{{18 + {x^2}}}{{x\left( {x - 3} \right)}}\) (ĐKXĐ: \(x \ne 0\,;\,\,x \ne 3).\) \(\frac{{x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)}} - \frac{{8\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} = \frac{{18 + {x^2}}}{{x\left( {x - 3} \right)}}\) \(x\left( {x + 3} \right) - 8\left( {x - 3} \right) = 18 + {x^2}\) \({x^2} + 3x - 8x + 24 = 18 + {x^2}\) \(8x - 3x = 24 - 18\) \(5x = 6\) \(x = \frac{6}{5}\) (TMĐK). Vậy phương trình đã cho có nghiệm là \(x = \frac{6}{5}.\)
|
Lời giải
Gọi giá niêm yết của một chiếc ti vi khi là \[x\] (triệu đồng) .
Giá niêm yết của một chiếc máy giặt là \[y\] (triệu đồng) \[\left( {0 < x,\,\,y < 28,5} \right).\]
Giá niêm yết một tivi và một máy giặt có tổng số tiền là \[28,5\] triệu đồng nên ta có phương trình:
\[x + y = 28,5.\] (1)
Sau khi giảm \[20\% \], giá của một chiếc ti vi là \[\left( {100\% - 20\% } \right)x = 0,8x\] (triệu đồng).
Khi giảm 25% ,giá của một chiếc máy giặt là: \[\left( {100\% - 25\% } \right)y = 0,75y\] (triệu đồng)
Theo bài ra ta có phương trình: \[0,8x\; + 0,75y\; = 22.\] (2)
Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 28,5\\0,8x\; + 0,75y\; = 22\end{array} \right.\].
Giải hệ phương trình trên, ta được \[\left\{ \begin{array}{l}x = 12,5\\y\; = 16\end{array} \right.\] (TMĐK).
Vậy giá niêm yết của một chiếc ti vi và máy giặt lần lượt là \[12,5\] triệu đồng và 16 triệu đồng.
Lời giải
1) a) Ta có \(C = \sin 30^\circ - \frac{{\tan 29^\circ }}{{\cot 61^\circ }} - 2{\cos ^2}60^\circ + \cot 45^\circ \)
\( = \frac{1}{2} - \frac{{\tan 29^\circ }}{{\tan 29^\circ }} - 2{\left( {\frac{1}{2}} \right)^2} + 1\)
\( = \frac{1}{2} - 1 - 2 \cdot \frac{1}{4} + 1 = 0.\)
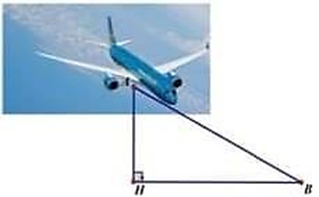
b) Xét \[\Delta ABH\] vuông tại \[H\] có: \(\sin B = \frac{{AH}}{{AB}} = \frac{{3,2}}{{6,8}} = \frac{8}{{17}}.\)
Suy ra \[\widehat B \approx 28^\circ .\]
2)
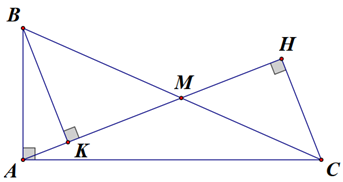
a) Vì tam giác \[ABC\] vuông tại \[A\] nên \(\widehat {BAC} = 90^\circ \); \(\widehat {ABC} + \widehat {ACB} = 90^\circ \).
Ta có \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) nên \(\widehat {ACB} = 90^\circ - \widehat {ABC} = 90^\circ - 53^\circ = 37^\circ .\)
Xét tam giác \[ABC\] vuông tại \[A\] có
• \(AC = AB \cdot \tan B = 6\tan 53^\circ \approx 8\,\,({\rm{cm}}).\)
• \(AC = BC \cdot \sin B\) suy ra \[BC = \frac{{AC}}{{\sin B}} = \frac{8}{{\sin 53^\circ }} \approx 10\,\,({\rm{cm}}).\]
b) Xét \[\Delta ABK\] và \[\Delta CAH\] có
\[\widehat {ABK} = \widehat {CAH}\] (cùng phụ \(\widehat {BAH}\,).\)
\[\widehat {AKB} = \widehat {AHC} = 90^\circ \]
Do đó (g.g).
Suy ra \[\frac{{BK}}{{AH}} = \frac{{AB}}{{AC}}\]
Do đó \[BK = AH \cdot \frac{{AB}}{{AC}} = AH \cdot \cot \widehat {ABC}\].
c) Ta có \(\frac{{MB}}{{MC}} = \frac{{BK}}{{CH}} = \frac{{AH \cdot \cot \widehat {ABC}}}{{CH}} = \frac{{AH \cdot \cot \widehat {ACB}}}{{CH}}.\)
Vì nên \(\frac{{KA}}{{HC}} = \frac{{AB}}{{AC}},\) suy ra \[\frac{1}{{HC}} = \frac{{AB}}{{AC}}:KA = \frac{{\tan ACB}}{{KA}}\].
Do đó \[\frac{{MB}}{{MC}} = \frac{{AH \cdot {{\tan }^2}\widehat {ACB}}}{{AK}}.\]
Lời giải
Đổi: 200 nghìn đồng \[ = 0,2\] triệu.
Gọi \[x\] (triệu đồng) là giá mới mà cửa hàng bán một chiếc máy tính \[(x > 18)\].
Số tiền cửa hàng bị giảm khi bán một chiếc máy tính là \[22--x\] ( triệu đồng).
Khi đó, số lượng máy tính bán ra được trong một năm là:
\[500 + 50\left( {22 - x} \right):0,2 = 6\,\,000 - 250x\] (chiếc)
Lợi nhuận mà doanh nghiệp thu được khi bán giá mới là
\[\left( {6\,\,000--250x} \right)\left( {x--18} \right) = - 250{x^2} + 10\,\,500x--108\,\,000\]
\[ = - 250\left( {{x^2}--42x + 432} \right)\]\[ = - 250{\left( {x - 21} \right)^2} + 2\,\,250 < 2\,\,250\].
Vậy giá bán mới một chiếc máy tính của cửa hàng là 21 triệu đồng, giá trị lợi nhuận thu được cao nhất là \[2\,\,250\] triệu đồng.