Bộ 5 đề thi cuối kì 2 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 5
26 người thi tuần này 4.6 184 lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 5
226 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 4
216 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 3
219 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 2
213 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 1
248 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 5
239 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 4
240 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 3
242 lượt thi
15 câu hỏi
Danh sách câu hỏi:
Đoạn văn 1
Câu 1-2. (2,0 điểm) Sau khi điều tra về số học sinh trong \[100\] lớp học (đơn vị: học sinh), người ta có bảng tần số ghép nhóm như ở bảng sau:
|
Nhóm |
\[\left[ {36\,\,;\,\,38} \right)\] |
\[\left[ {38\,\,;\,\,40} \right)\] |
\[\left[ {40\,\,;\,\,42} \right)\] |
\[\left[ {42\,\,;\,\,44} \right)\] |
\[\left[ {44\,\,;\,\,46} \right)\] |
|
Tần số \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Lời giải
a) Tần số tương đối của các nhóm lần lượt là:
;
; ;
Đoạn văn 5
Câu 12-13. (1,5 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít ba quả bóng tennis xếp theo chiều dọc (hình vẽ). Các quả bóng tennis có dạng hình cầu, đường kính \(6,4\;{\rm{cm}}\).
Lời giải
b) Bảng tần số tương đối của mỗi nhóm
|
Nhóm |
\[\left[ {36\,;\,38} \right)\] |
\[\left[ {38\,;40} \right)\] |
\[\left[ {40\,;42} \right)\] |
\[\left[ {42\,;\,44} \right)\] |
\[\left[ {44\,;46} \right)\] |
|
Tần số tương đối \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Biểu đồ cột của mẫu số liệu ghép nhóm:
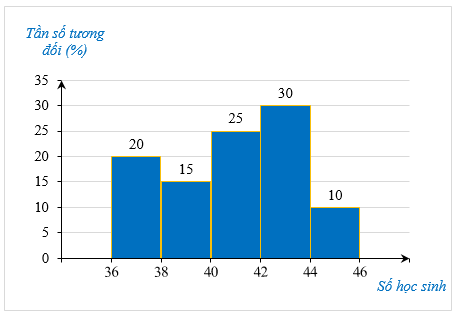
Lời giải
a) Chiều cao hộp dựng bóng hình trụ là \(h = 6,4 \cdot 3 = 19,2\,\,(\;{\rm{cm}})\)
Bán kính đáy hộp đựng bóng hình trụ là \({R_1} = 6,4:2 = 3,2\,\,(\;{\rm{cm}})\).
Thể tích hộp đựng bóng hình trụ là:
\({V_1} = \pi rR_1^2\;h = \pi \cdot 3,{2^2} \cdot 19,2 = 618\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Vậy thể tích hộp dựng bóng \(618\,\,{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
b) Bán kính quả bóng tennis là \({R_2} = \frac{{6,4}}{2} = 3,2\,\,\left( {cm} \right)\).
Thể tích của ba quả bóng tennis có dạng hình cầu là:
\({V_2} = 3.\left( {\frac{4}{3}\pi R_2^3} \right) = 3 \cdot \left( {\frac{4}{3}\pi \cdot 3,{2^3}} \right) \approx 412\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis là:
\(V = {V_1} - {V_2} = 618 - 412 = 206\,\,\left( {c{m^3}} \right)\).
Vậy thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis \(206\,\,c{m^3}.\)
Đoạn văn 2
Câu 3-4. (1,5 điểm) Hộp thứ nhất đựng 1 quả bóng trắng, 1 quả bóng đó. Hộp thứ 2 đựng 1 quả bóng đó, 1 quả bóng vàng. Lấy ra ngẫu nhiên từ mỗi hộp 1 quả bóng.
Lời giải
a) Kí hiểu \[T\] là màu trắng, là màu đỏ và \[V\] là màu vàng.
Không gian mẫu .
Số kết quả có thể xảy ra là \(n\left( \Omega \right) = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Câu 5-6. Cho đồ thị hàm số \(\left( P \right):y = 5{x^2}\). Xác định điểm thuộc đồ thị hàm số \(\left( P \right)\) thỏa mãn:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Câu 9-11. Cho đường tròn \(\left( O \right)\), bán kính \(R\,\,\left( {R > 0} \right)\) và dây cung \(BC\) cố định. Một điểm \(A\) chuyển động trên cung lớn \(BC\) sao cho tam giác \(ABC\) có ba góc nhọn. Kẻ các đường cao \(AD,\,\,BE\) của tam giác \(ABC\) cắt nhau tại \(H\) và \(BE\) cắt đường tròn \(\left( O \right)\) tại ( F khác B)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập