Giải SBT Toán 8 CTST Định lí Thalès trong tam giác có đáp án
51 người thi tuần này 4.6 666 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 02
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 01
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Danh sách câu hỏi:
Lời giải

Đặt AB = BC = CD = a, ta có:
• \[\frac{{AB}}{{BD}} = \frac{{AB}}{{BC + CD}} = \frac{a}{{a + a}} = \frac{a}{{2a}} = \frac{1}{2}\];
• \[\frac{{AB}}{{AD}} = \frac{{AB}}{{AB + BC + CD}} = \frac{a}{{a + a + a}} = \frac{a}{{3a}} = \frac{1}{3}\];
• \[\frac{{AC}}{{AD}} = \frac{{AB + BC}}{{AB + BC + CD}} = \frac{{a + a}}{{a + a + a}} = \frac{{2a}}{{3a}} = \frac{2}{3}\].
Lời giải

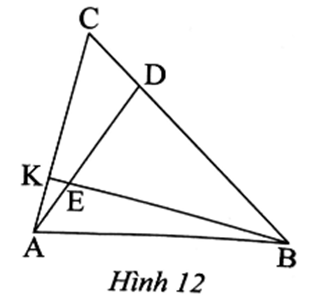
a) Ta có \[\frac{{CA}}{{CB}} = \frac{3}{2}\], suy ra: \[\frac{{CA}}{3} = \frac{{CB}}{2}\].
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{CA}}{3} = \frac{{CB}}{2} = \frac{{CA + CB}}{{3 + 2}} = \frac{{AB}}{5} = \frac{{10}}{5} = 2\].
Nên \[\frac{{CB}}{2} = 2 \Rightarrow CB = 2.2 = 4\] (cm).
b) Ta có \[\frac{{DA}}{{DB}} = \frac{3}{2}\], suy ra \[\frac{{DA}}{3} = \frac{{DB}}{2}\].
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{DA}}{3} = \frac{{DB}}{2} = \frac{{DA - DB}}{{3 - 2}} = \frac{{AB}}{1} = \frac{{10}}{1} = 10\].
Nên \[\frac{{DB}}{2} = 10 \Rightarrow DB = 10.2 = 20\](cm).
c) Ta có CD = CB + BD = 4 + 20 = 24 (cm).
Lời giải
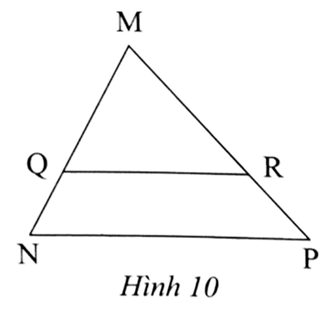
Xét ∆MNP, có QR // NP, nên theo định lí Thalès, ta có \[\frac{{MQ}}{{QN}} = \frac{{MR}}{{RP}}\].
Suy ra \[MR = \frac{{MQ.RP}}{{QN}} = \frac{{10.6}}{5} = 12\](cm).
Vậy MR = 12 cm.
Lời giải
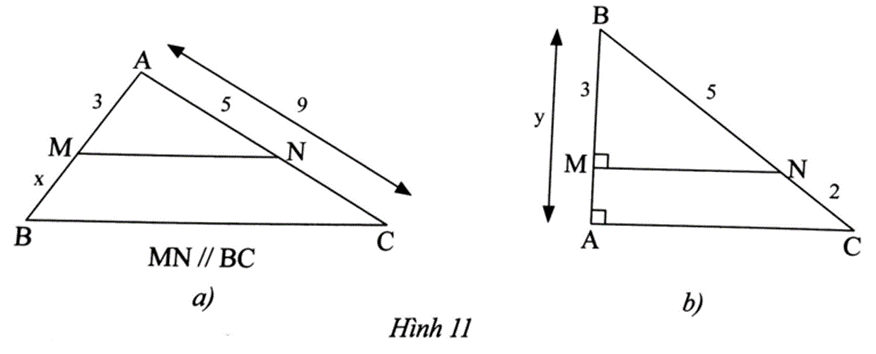
a) Ta có CN = AC – AN = 9 – 5 = 4.
Xét ∆ABC, có MN // BC, nên theo định lí Thalès, ta có \[\frac{{AM}}{{BM}} = \frac{{AN}}{{CN}}\].
Suy ra \[BM = \frac{{AM.CN}}{{AN}} = \frac{{3.4}}{5} = 2,4\].
Vậy x = 2,4.
b) ) Ta có BC = BN + NC = 5 + 2 = 7.
Vì MN và AC cùng vuông góc với AB nên MN song song với AC.
Xét ∆ABC, có MN // AC, nên theo định lí Thalès, ta có \[\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}}\].
Suy ra \[AB = \frac{{BM.BC}}{{BN}} = \frac{{3.7}}{5} = 4,2\].
Vậy y = 4,2.
Lời giải
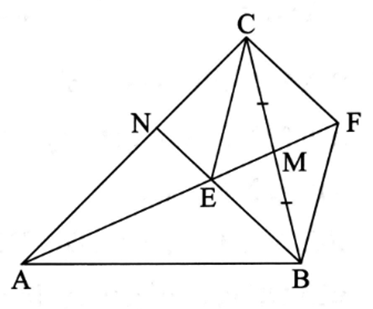
Lấy điểm F trên tia AM sao cho M là trung điểm của EF.
Tứ giác MEFC có hai hai đường chéo BC và EF cắt nhau tại trung điểm của mỗi đường nên tứ giác MEFC là hình bình hành.
Suy ra CF // BE và CF // EN.
Ta có AE = 3EM và ME = MF (vì M là trung điểm của EF).
Khi đó, \[\frac{{AE}}{{EF}} = \frac{3}{2}\].
Xét ∆ACF có CF // EN nên theo định lí Thalès, ta có: \[\frac{{AN}}{{NC}} = \frac{{AE}}{{EF}} = \frac{3}{2}\].
Vậy \[\frac{{AN}}{{NC}} = \frac{3}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.