Giải SGK Toán 12 CTST Bài 2. Công thức xác suất toàn phần và công thức Bayes có đáp án
51 người thi tuần này 4.6 1.2 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Sau khi học xong bài này, ta giải quyết bài toán này như sau:
Gọi A là biến cố “Người làm xét nghiệm có kết quả dương tính” và B là biến cố “Người làm xét nghiệm thực sự nhiễm vi rút”.
Ta có P(A|B) = 0,762; \(P\left( {\overline A |\overline B } \right) = 0,991\); P(B) = 0,01.
Suy ra \(P\left( {A|\overline B } \right) = 1 - P\left( {\overline A |\overline B } \right) = 0,009\), \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 0,99\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\) = 0,01.0,762 + 0,99.0,009 = 0,01653.
Xác suất một người thực sự nhiễm virus khi người đó có kết quả xét nghiệm dương tính là P(B|A).
Ta có \(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,01.0,762}}{{0,01653}} \approx 0,461\).
Vậy khả năng thực sự người đó nhiễn virus là 46,1%.
Lời giải
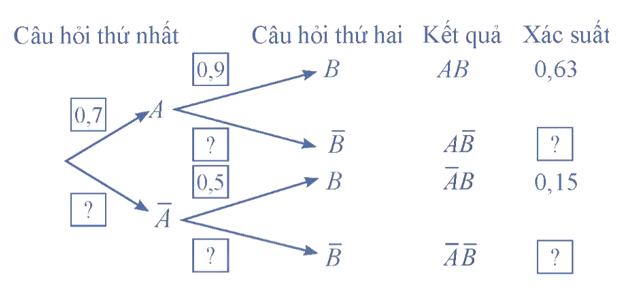
A là biến cố “Chị An trả lời đúng câu hỏi thứ nhất” và B là biến cố “Chị An trả lời đúng câu hỏi thứ hai”.
Ta có P(A) = 0,7; P(B|A) = 0,9; \(P\left( {B|\overline A } \right) = 0,5\).
Suy ra \(P\left( {\overline A } \right) = 1 - P\left( A \right) = 0,3;P\left( {\overline B |A} \right) = 1 - P\left( {B|A} \right) = 0,1\);
\(P\left( {\overline B |\overline A } \right) = 1 - P\left( {B|\overline A } \right) = 0,5\)
Ta có sơ đồ hình cây
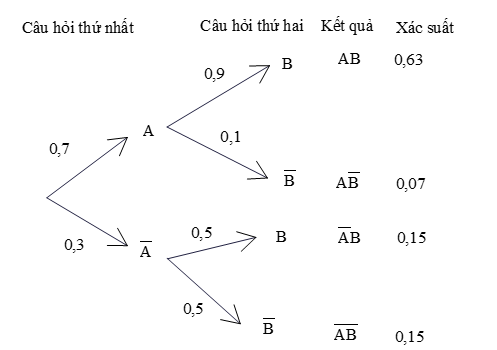
Lời giải
Gọi A là biến cố “Tuyến phố H bị tắc đường” và B là biến cố “Buổi sáng đó có mưa”
Theo đề ta có: P(B) = 0,1; P(A|B) = 0,7; \(P\left( {A|\overline B } \right) = 0,2\).
Suy ra \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 0,9\).
Áp dụng công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\) = 0,1.0,7 + 0,9.0,2 = 0,25.
Lời giải
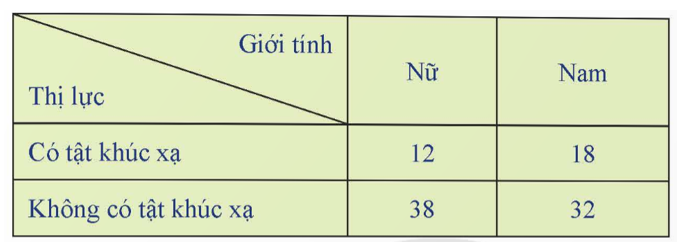
Gọi A là biến cố “Học sinh đó có tật khúc xạ” và B là biến cố “Học sinh đó là học sinh nam”.
a) Ta có \(P\left( {B|A} \right) = \frac{{18}}{{12 + 18}} = \frac{3}{5}\).
b) Ta có \(P\left( {A|B} \right) = \frac{{18}}{{18 + 32}} = \frac{9}{{25}}\).
Lời giải
Gọi A là biến cố “Hệ thống radar phát cảnh báo” và B là biến cố “Vật thể bay đó là mục tiêu thật”.
Theo đề ta có P(A|B) = 0,9; \(P\left( {A|\overline B } \right) = 0,05\); \(P\left( {\overline B } \right) = 0,99\).
Suy ra \(P\left( B \right) = 1 - P\left( {\overline B } \right) = 0,01\).
Ta có \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\) = 0,01.0,9 + 0,99.0,05 = 0,0585.
Ta cần tính \(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,01.0,9}}{{0,0585}} = \frac{2}{{13}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.