Giải SGK Toán 8 CTST Bài tập cuối chương 3 có đáp án

Đáp án đúng là: D

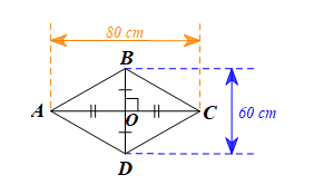
Hình ảnh khung diều hình thoi được mô phỏng bởi hình thoi ABCD có các kích thước như hình vẽ trên.

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra $OB=\frac{1}{2}BD=\frac{1}{2}.60=30\left(cm\right)$ và $OA=\frac{1}{2}AC=\frac{1}{2}.80=40\left(cm\right)$.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB² = 40² + 30² = 1 600 + 900 = 2 500 = 50²

Suy ra AB = 50 cm.

Do vậy cạnh của hình thoi có độ dài 50 cm.

Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:

4.50 = 200 cm = 2 m.

Đáp án đúng là: A

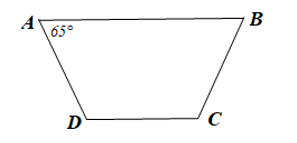
Do ABCD là hình thang cân (AB // CD) nên $\widehat{A}+\widehat{D}=180°$

Suy ra $\widehat{D}=180°-\widehat{A}=180°-65°=115°$.

Mặt khác, ABCD là hình thang cân (AB // CD) nên $\widehat{C}=\widehat{D}=115°$.

Đáp án đúng là: C

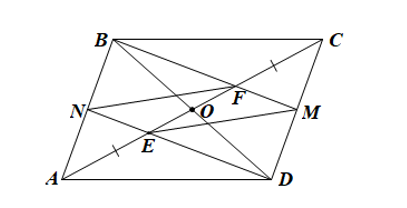
Theo tính chất hình bình hành: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Do đó đây là tính chất đã có sẵn của hình bình hành, nên khẳng định C là sai.

Đáp án đúng là: A

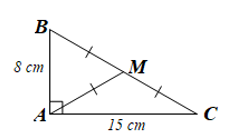
Áp dụng định lí Pythagore vào DABC vuông tại A ta có:

BC² = AB² + AC² = 8² + 15² = 64 + 225 = 289 = 17².

Suy ra BC = 17 cm.

Xét tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC.

Do đó $AM=\frac{1}{2}BC=\frac{1}{2}.17=8,5\left(cm\right)$.

Đáp án đúng là: A

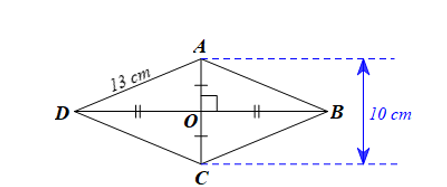
Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra $OD=\frac{1}{2}BD$ và $OA=\frac{1}{2}AC=\frac{1}{2}.10=5\left(cm\right)$.

Áp dụng định lí Pythagore vào DOAD vuông tại O, ta có:

AD² = OA² + OD²

Suy ra $OD=\sqrt{A{D}^2-O{A}^2}=\sqrt{{13}^2-5^2}=12\left(cm\right)$.

Do đó BD = 2OD = 2.12 = 24 (cm).

Đáp án đúng là: C

Theo tính chất của hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và có bốn góc vuông. Do đó đây là các tính chất đã có sẵn của hình chữ nhật nên A và D là khẳng định sai.

Theo tính chất của hình thoi: Hình thoi có hai đường chéo vuông góc với nhau. Do đó đây là tính chất đã có sẵn của hình thoi nên B là khẳng định sai.

Hình thoi có một góc vuông là hình vuông. Đây là khẳng định đúng.

Đáp án đúng là: A

Xét tứ giác ABCD có $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (tổng các góc của một tứ giác).

Suy ra $\widehat{C}=360°-\left(\widehat{A}+\widehat{B}+\widehat{D}\right)$

Do đó $\widehat{C}=360°-\left(60°+110°+70°\right)=120°$.

a) • Ta có: AE = EF = FC nên $AE=EF=FC=\frac{1}{3}AC$   (1)

Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành.

Khi đó O là trung điểm của AC và BD.

Suy ra $AO=CO=\frac{1}{2}AC$   (2)

Từ (1) và (2) suy ra $\frac{CF}{CO}=\frac{\frac{1}{3}AC}{\frac{1}{2}AC}=\frac{2}{3}$ hay $CF=\frac{2}{3}CO$.

• Xét DBCD có CO là trung tuyến của tam giác và $CF=\frac{2}{3}CO$ nên F là trọng tâm của DBCD.

Do đó BF hay BM cũng là đường trung tuyến của DBCD.

Suy ra M là trung điểm của CD.

• Chứng minh tương tự đối với DABD ta có E là trọng tâm của tam giác.

Do đó DE hay DN cũng là đường trung tuyến của DABD.