10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

Đáp án đúng là: A

Vì SA ^ (ABCD) ⇒ SA ^ BC.

Ta có: $\left\{\begin{array}{l}BC\perp AB\\ BC\perp SA\end{array}\right.\Rightarrow BC\perp \left(SAB\right)\Rightarrow BC\perp SB$ .

Đáp án đúng là: A

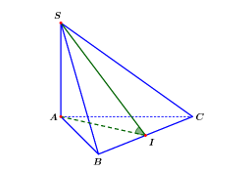
Gọi I là trung điểm BC ⇒ AI ^ BC (vì ABC là tam giác đều) (1).

Vì SA ^ (ABC) ⇒ SA ^ BC (2).

Từ (1) và (2) ⇒ BC ^ (SAI) ⇒ BC ^ SI.

Khi đó:$\left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ SI\perp BC\\ AI\perp BC\end{array}\right.\Rightarrow \left[S,BC,A\right]=\widehat{SIA}$ .

Mà DABC đều cạnh a nên $AI=\frac{a\sqrt{3}}{2}$  .

Xét DSAI vuông tại A, ta có: $\text{tan}\widehat{SIA}=\frac{SA}{AI}=\sqrt{3}\Rightarrow \widehat{SIA}=60°$ .

Đáp án đúng là: C

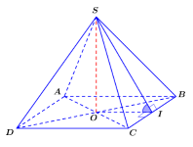
Gọi O là tâm của hình vuông ABCD và I là trung điểm của BC. Suy ra OI ^ BC.

Vì S.ABCD là hình chóp tứ giác đều nên SO ^ (ABCD) và  $SO=\frac{a}{2\sqrt{3}}$.

Và SC = SB nên tam giác SBC cân tại S ⇒ SI ^ BC.

Ta có: $SO=\frac{a}{2\sqrt{3}}\Rightarrow \left[S,BC,A\right]=\widehat{SIO}$ .

Ta có: OI là đường trung bình tam giác ABC nên $\Rightarrow \left[S,BC,A\right]=\widehat{SIO}$ .

Xét DSIO vuông tại O, ta có: $\tan \widehat{SIO}=\frac{SO}{OI}=\frac{\sqrt{3}}{3}\Rightarrow \widehat{SIO}=30°$ .

Vậy số đo góc phẳng nhị diện [S, BC, A] bằng 30°.

Hướng dẫn giải:

Đáp án đúng là: B

Gọi I là trung điểm của BC.

Vì DOBC vuông cân tại O ⇒ OI ^ BC (1).

Vì OA ^ OB và OA ^ OC nên OA ^ (OBC) ⇒ OA ^ BC (2).

Từ (1) và (2), suy ra BC ^ (AOI) ⇒ BC ^ AI

Khi đó: $\left\{\begin{array}{l}\left(OBC\right)\cap \left(ABC\right)=BC\\ BC\perp AI\\ BC\perp OI\end{array}\right.\Rightarrow \left[O,BC,A\right]=\widehat{OIA}$  .

Và $OI=\frac{1}{2}BC=\frac{1}{2}\sqrt{O{B}^2+O{C}^2}=a\sqrt{3}$ .

Xét DOAI vuông tại O, ta có: $OI=\frac{1}{2}BC=\frac{1}{2}\sqrt{O{B}^2+O{C}^2}=a\sqrt{3}$ .

Vậy [O, BC, A] = 30°.

Đáp án đúng là: D

Gọi O là tâm của hình vuông ABCD và I trung điểm của BC. Suy ra OI ^ BC.

Khi đó: SO ^ (ABCD) ⇒ SO ^ BC mà OI ^ BC nên BC ^ (SOI) ⇒ BC ^ SI.

Ta có: $\left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ BC\perp SI\\ BC\perp OI\end{array}\right.\Rightarrow \left[S,BC,A\right]=\widehat{SIO}$ .

Và DSCD đều cạnh a ⇒ $SI=\frac{a\sqrt{3}}{2}$ .

OI là đường trung bình của DACB ⇒  $OI=\frac{a}{2}$.

Xét DSOI vuông tại O, ta có: $\cos \widehat{SIO}=\frac{OI}{SI}=\frac{\sqrt{3}}{3}$.

Đáp án đúng là: B

Gọi H, K lần lượt là trung điểm của AD, BC.

Vì DSAD đều nên SH ^ AD mà (SAD) ^ (ABCD) ⇒ SH ^ (ABCD) ⇒ SH ^ BC.

Lại có HK ^ BC nên BC ^ (SHK) ⇒ BC ^ SK.

Ta có: $\left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ HK\perp BC\\ SK\perp BC\end{array}\right.\Rightarrow \left[S,BC,A\right]=\widehat{SKH}=\phi$  .

Vì DSAD đều cạnh a nên $SH=\frac{a\sqrt{3}}{2}$và HK = AB = 2a

Xét DSHK vuông tại H, ta có:

$\tan \phi =\tan \widehat{SKH}=\frac{SH}{HK}=\frac{\sqrt{3}}{4}$.

Đáp án đúng là: D

Vì SA ^ (ABC) ⇒ SA ^ BC.

Mà BC ^ AB (do DABC vuông cân tại B). Suy ra BC ^ (SAB) ⇒ BC ^ SB.

Khi đó: $\left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ BC\perp AB\\ BC\perp SB\end{array}\right.\Rightarrow \left[S,BC,A\right]=\widehat{SBA}$

Xét DSAB vuông tại A, ta có: $\tan \widehat{SBA}=\frac{SA}{AB}=\frac{a\sqrt{3}}{a}=\sqrt{3}\Rightarrow \widehat{SBA}=60°$ .

Đáp án đúng là: A

Gọi O là tâm của hình vuông ABCD. Suy ra O là trung điểm của AC và BD.

Vì ABCD là hình vuông nên AO ^ BD.

Vì SA ^ (ABCD) ⇒ SA ^ BD mà AO ^ BD nên BD ^ (SOA) ⇒ BD ^ SO.

Khi đó:$\left\{\begin{array}{l}\left(SBD\right)\cap \left(ABD\right)=BD\\ OA\perp BD\\ SO\perp BD\end{array}\right.\Rightarrow \left[S,BD,A\right]=\widehat{SOA}$   .

Xét DABC vuông tại B, có $AC=\sqrt{A{B}^2+B{C}^2}=a\sqrt{2}\Rightarrow AO=\frac{a\sqrt{2}}{2}$ .

Xét DSOA vuông tại A, ta có:  $\tan \widehat{SOA}=\frac{SA}{OA}=\frac{\frac{a\sqrt{6}}{6}}{\frac{a\sqrt{2}}{2}}=\frac{\sqrt{3}}{3}\Rightarrow \widehat{SOA}=30°$

Vậy góc phẳng nhị diện [S, BD, A] bằng 30°.

Đáp án đúng là: A

Đáp án đúng là: D

Gọi O là giao điểm của AC và BD. Suy ra O là trung điểm của AC và BD.

Vì SA = SC nên DSAC cân tại S, SO là trung tuyến nên SO ^ AC (1).

Vì SB = SD nên DSBD cân tại S, SO là trung tuyến nên SO ^ BD (2).

Từ (1) và (2), suy ra SO ^ (ABCD).

Gọi M là trung điểm của BC.

Ta có OM là đường trung bình của DABC ⇒ $OM=\frac{AB}{2}=2a$ .

Xét DABC vuông tại B, có $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{16a^2+9a^2}=5a$ .

Vì O là trung điểm AC nên $AO=CO=\frac{AC}{2}=\frac{5a}{2}$ .

Xét DSOA vuông tại O, có $SO=\sqrt{S{A}^2-A{O}^2}=\sqrt{25a^2-\frac{25a^2}{4}}=\frac{5\sqrt{3}a}{2}$.

Vì SO ^ (ABCD) ⇒ SO ^ BC mà OM ^ BC ⇒ BC ^ (SOM) ⇒ BC ^ SM.

Khi đó $\left.\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ OM\perp BC\\ SM\perp BC\end{array}\right\}\Rightarrow [S,BC,A]=\widehat{SMO}$ .