Giải SBT Toán 12 Tập 1 KNTT Bài tập cuối chương II có đáp án
39 người thi tuần này 4.6 612 lượt thi 16 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
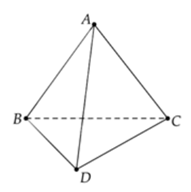
Các vectơ thỏa mãn là: \(\overrightarrow {AB} \), \(\overrightarrow {AC} \), \(\overrightarrow {BC} \), \(\overrightarrow {BA} \), \(\overrightarrow {CA} \), \(\overrightarrow {CB} \).
Vậy có 6 vectơ thỏa mãn yêu cầu bài toán.
Lời giải
Đáp án đúng là: D
Các vectơ đối của \(\overrightarrow a \) đều bằng nhau và bằng \(\left| {\overrightarrow a } \right|\).
Lời giải
Đáp án đúng là: C
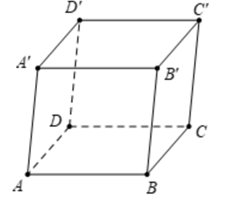
Có tứ giác ACC'A' là hình chữ nhật nên \(\overrightarrow {AA'} + \overrightarrow {AC} = \overrightarrow {AC'} \).
Lời giải
Đáp án đúng là: D
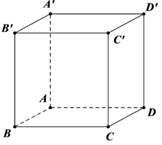
Ta có: \(\overrightarrow {AB} .\overrightarrow {B'D'} \) = \(\overrightarrow {AB} .\overrightarrow {BD} \)
= \(\overrightarrow {AB} \left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\)
= \(\overrightarrow {AB} .\overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {BC} \)
= 2.2.cos180° − 2.2.cos90° = −4.
Lời giải
Đáp án đúng là: B
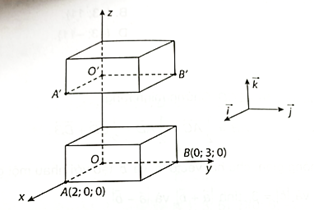
Gọi G(x; y; z) là trọng tâm tam giác ABC, ta có:
\(\left\{ \begin{array}{l}x = \frac{{1 + 0 + 5}}{3} = 2\\y = \frac{{3 + 6 + 3}}{3} = 4\\z = \frac{{5 + ( - 2) + 6}}{3} = 3\end{array} \right.\)
Vậy G(2; 4; 3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.