Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 2
27 người thi tuần này 4.6 490 lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Đoạn văn 1
(2,0 điểm) Cho hai biểu thức và .
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{1}{3} - \frac{1}{{\sqrt x }}\).
Điều kiện xác định của biểu thức \(A\) là \(x \ge 0\) và \(\sqrt x \ne 0\), tức là \(x > 0.\)
⦁ Xét biểu thức \(B = \frac{{\sqrt x + 3}}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\).
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,\sqrt x - 3 \ne 0\) và \(\sqrt x + 3 \ne 0.\)
Với \(x \ge 0\) ta thấy \(\sqrt x + 3 > 0\) và \(\sqrt x - 3 \ne 0\) khi \(x \ne 9.\)
Vậy điều kiện xác định của biểu thức \(A\) là \(x > 0\) và điều kiện xác định của biểu thức \(B\) là \(x \ge 0\), \(x \ne 9.\)
Lời giải
b) Thay \(x = \frac{1}{9}\) (thỏa mãn điều kiện) vào biểu thức \(A\), ta được:
\(A = \frac{1}{3} - \frac{1}{{\sqrt {\frac{1}{9}} }} = \frac{1}{3} - \frac{1}{{\frac{1}{3}}} = \frac{1}{3} - 3 = - \frac{8}{3}.\)
Vậy giá trị biểu thức \(A = - \frac{8}{3}\) tại \(x = \frac{1}{9}.\)
Lời giải
c) Với \(x \ge 0;x \ne 9\), ta có:
\(B = \frac{{\sqrt x + 3}}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\)
\( = \frac{{{{\left( {\sqrt x + 3} \right)}^2} - {{\left( {\sqrt x - 3} \right)}^2}}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \frac{{x + 6\sqrt x + 9 - \left( {x - 6\sqrt x + 9} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \frac{{x + 6\sqrt x + 9 - x + 6\sqrt x - 9}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \frac{{12\sqrt x }}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{12\sqrt x }}{{x - 9}}.\)
Vậy với \(x \ge 0;x \ne 9\) thì \(B = \frac{{12\sqrt x }}{{x - 9}}.\)
Lời giải
d) Với \(x > 0;x \ne 9\), ta có:
\(P = A \cdot B = \left( {\frac{1}{3} - \frac{1}{{\sqrt x }}} \right) \cdot \frac{{12\sqrt x }}{{x - 9}}\) \( = \frac{{\sqrt x - 3}}{{3\sqrt x }}.\frac{{12\sqrt x }}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\)\( = \frac{4}{{\sqrt x + 3}}\).
Với \(x > 0;x \ne 9\), ta có \(\sqrt x > 0\) nên \(\sqrt x + 3 > 3\), suy ra \(\frac{4}{{\sqrt x + 3}} < \frac{4}{3}\).
Ta cũng có: \(\sqrt x + 3 > 3 > 0\) nên \(\frac{4}{{\sqrt x + 3}} > 0\).
Do đó \(0 < P < \frac{4}{3}.\)
Như vậy, để \(P\) nguyên thì \(P = 1\).
Khi đó, ta có: \(\frac{4}{{\sqrt x + 3}} = 1,\) suy ra \(\sqrt x + 3 = 4\) nên \(\sqrt x = 1,\) suy ra \(x = 1\) (thỏa mãn điều kiện).
Vậy với \(x = 1\) thì \(P\) nhận giá trị nguyên.
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định \(x \ne \frac{1}{3},\,\,x \ne - \frac{1}{3}.\)
Ta có: \(\frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}} = \frac{4}{{1 - 9{x^2}}}\)
\(\frac{{{{\left( {1 - 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} - \frac{{{{\left( {1 + 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} = \frac{4}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}}\)
\(\frac{{{{\left( {1 - 3x} \right)}^2} - {{\left( {1 + 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} = \frac{4}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}}\)
\({\left( {1 - 3x} \right)^2} - {\left( {1 + 3x} \right)^2} = 4\)
\(\left( {1 - 3x - 1 - 3x} \right)\left( {1 - 3x + 1 + 3x} \right) = 4\)
\( - 6x \cdot 2 = 4\)
\( - 12x = 4\)
\(x = - \frac{1}{3}\) (loại).
Vậy phương trình vô nghiệm.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
2. Giải bài toán sau bằng cách lập hệ phương trình:
Để chuẩn bị cho chuyến đi dã ngoại của gia đình, cô Linh đi siêu thị mua 1 thùng nước ngọt và 4 túi bánh mì sandwich với giá niêm yết tổng cộng là 340 000 đồng. Tuy nhiên khi đến siêu thị thì cô Linh được biết giá mỗi thùng nước ngọt tăng \(5\% \) và giá mỗi túi bánh mì sandwich được giảm \(15\% \) so với giá niêm yết nên cô Mai đã trả tổng cộng 325 000 đồng. Tính giá niêm yết của một thùng nước ngọt và giá niêm yết của một túi bánh mì sandwich.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Để chuẩn bị cho chuyến đi dã ngoại của gia đình, cô Linh đi siêu thị mua 1 thùng nước ngọt và 4 túi bánh mì sandwich với giá niêm yết tổng cộng là 340 000 đồng. Tuy nhiên khi đến siêu thị thì cô Linh được biết giá mỗi thùng nước ngọt tăng \(5\% \) và giá mỗi túi bánh mì sandwich được giảm \(15\% \) so với giá niêm yết nên cô Mai đã trả tổng cộng 325 000 đồng. Tính giá niêm yết của một thùng nước ngọt và giá niêm yết của một túi bánh mì sandwich.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
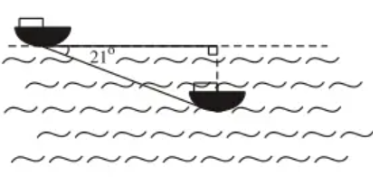
(1,5 điểm) Trong một buổi luyện tập, một tàu ngầm ở trên mặt biển bắt đầu lặn xuống và di chuyển theo một đường thẳng tạo với mặt nước một góc \(21^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho hai tiếp tuyến \(AB\) và \(AC\) của đường tròn tâm \(O\) (\(B,C\) là hai tiếp điểm). Vẽ đường kính \(BD\), \(AO\) cắt \(BC\) tại \(H\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.