Giải SBT Toán 9 CTST Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông

Gọi tam giác ABC là tam giác vuông tại A có BC = 25 cm và $\widehat{C}=29°.$

Ta có: AB = BC.sinC = 25.sin29° ≈ 12,12 (cm);

           AC = BC.cosC = 25.cos29° ≈ 21,87 (cm).

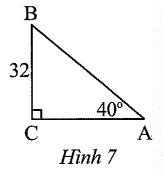
Xét ∆ABC vuông tại C có:

AC = BC.cotA = 32.cot 40° ≈ 38,14.

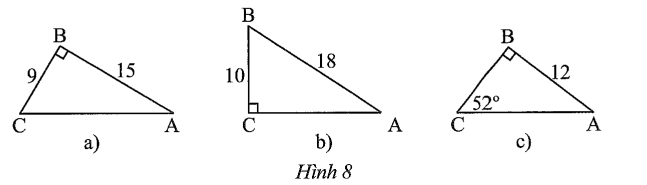
a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:

 $AC=\sqrt{B{A}^2+B{C}^2}=\sqrt{{15}^2+9^2}=\sqrt{306}\approx 17,49.$

Xét ∆ABC vuông tại B, ta có:

⦁ $\tan A=\frac{BC}{BA}=\frac{9}{15}=0,6,$  suy ra $\widehat{A}\approx 30°{58}^{\text{'}}.$

⦁ $\widehat{A}+\widehat{C}=90°$  (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{C}=90°-\widehat{A}\approx 90°-30°{58}^{\text{'}}=59°2^{\text{'}}.$

b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:$AC=\sqrt{A{B}^2-B{C}^2}=\sqrt{{18}^2-{10}^2}=\sqrt{224}\approx 14,97.$

Xét ∆ABC vuông tại C, ta có:

⦁ $\sin A=\frac{BC}{AB}=\frac{10}{18}=\frac{5}{9},$  suy ra  $\widehat{A}\approx 33°{45}^{\text{'}}.$

⦁ $\widehat{A}+\widehat{B}=90°$  (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{B}=90°-\widehat{A}\approx 90°-33°{45}^{\text{'}}=56°{15}^{\text{'}}.$

c) Xét ∆ABC vuông tại B, ta có:

⦁ $\widehat{A}+\widehat{C}=90°$  (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{A}=90°-\widehat{C}=90°-52°=38°.$

⦁ BC = AB.tanA = 12.tan38° ≈ 9,38.

⦁ AB = AC.sinC, suy ra $AC=\frac{AB}{\sin C}=\frac{12}{\sin 52°}\approx 15,23.$

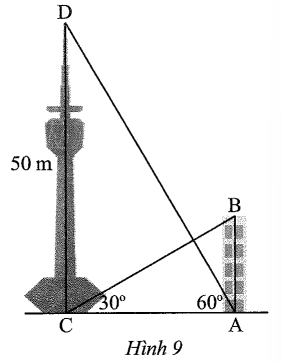
Ta có chiều cao của tòa nhà và tháp lần lượt là AB, CD (đơn vị: m, AB > 0).

Khi đó,$\widehat{ACB}=30°,\widehat{CAD}=60°.$

Xét tam giác ACD vuông tại C, ta có:$AC=DC\cdot \cot \widehat{CAD}=50\cdot \cot 60°=\frac{50\sqrt{3}}{3}\left(\text{m}\right).$

Xét tam giác ABC vuông tại A, ta có:$AB=AC\cdot \tan \widehat{ACB}=\frac{50\sqrt{3}}{3}\cdot \tan 30°=\frac{50\sqrt{3}}{3}\cdot \frac{\sqrt{3}}{3}=\frac{50}{3}\approx 16,67\left(\text{m}\right).$

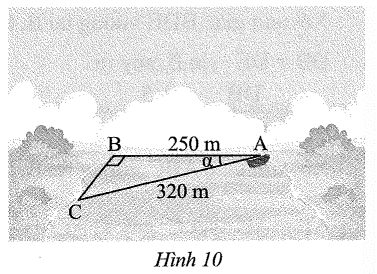
Xét tam giác ABC vuông tại B, ta có: $\cos \widehat{BAC}=\frac{AB}{AC}=\frac{250}{320}=0,78125,$ suy ra$\widehat{BAC}\approx 38°{37}^{\text{'}}.$

Vậy chiếc thuyền đó bị dòng nước đẩy lệch một góc khoảng 38°37’ so với dự tính.