Cho khối trụ có hai đáy là (O) và (O′). AB,CD lần lượt là hai đường kính của (O) và (O′), góc giữa AB và CD bằng 300, AB = 6 và thể tích khối tứ diện ABCD bằng 30. Thể tích khối trụ đã cho bằng:
A.\(180\pi \)
B. \(90\pi \)
C. \(30\pi \)
D. \(45\pi \)
Quảng cáo
Trả lời:
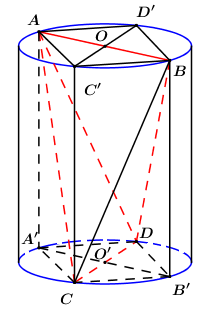
Gọi A′,B′ lần lượt là hình chiếu của A,B lên đường tròn (O).
C′,D′ lần lượt là hình chiếu của C,D lên đường tròn (O′).
=>AC′BD′ là hình bình hành, lại có AB = CD = C′D′ nên AC′BD′ là hình chữ nhật.
Khi đó AC′BD′.A′CB′D là hình hộp chữ nhật.
Ta có:\[{V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\]
Ta có:\[{V_{A.A'CD}} = \frac{1}{3}AA'.{S_{A'CD}} = \frac{1}{3}AA'.\frac{1}{2}{S_{A'CB'D}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]
CMTT ta có: \[{V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\frac{1}{6}{V_{AC'BD'.A'CB'D}}}\\{ \Rightarrow {V_{ABCD}} = \frac{1}{3}{V_{AC'BD'.A'CB'D}} = 30}\\{ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90}\end{array}\]
Theo bài ra ta có: \[\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\]giả sử\[\angle \left( {AB;C'D'} \right) = \angle \[ \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\]Lại có \[OA = OC' = \frac{1}{2}AB = 3\]
\[ \Rightarrow {S_{OAC'}} = \frac{1}{2}OA.OC'.\sin \angle AOC' = \frac{1}{2}.3.3.\sin {30^0} = \frac{9}{4}\]
Ta có: \[{V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}} \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\]
Vậy thể tích khối trụ là \[V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \]
Đáp án cần chọn là: B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.280 ngày
B.281 ngày
C.282 ngày
D.882 ngày
Lời giải
Thể tích gáo \[{V_1} = \pi {R^2}.h = \pi .0,{04^2}.0,05 = 8\pi {.10^{ - 5}}({m^3})\]
Số nước múc ra trong một ngày \[{V_2} = 170{V_1} = 170.8.\pi {.10^{ - 5}} = 0,0136\pi \left( {{m^3}} \right)\]
Số ngày dùng hết nước là \[\frac{{2.3.2}}{{{V_2}}} = \frac{{12}}{{0,0136\pi }} \approx 281\] (ngày)
Đáp án cần chọn là: B
Câu 2
A.đường tròn
B.hình chữ nhật
C.hình thang cân
D.elip
Lời giải
Khi cắt mặt trụ bởi mặt phẳng tạo với trục một góc \[\alpha ({0^0} < \alpha < {90^0})\] thì ta được elip.
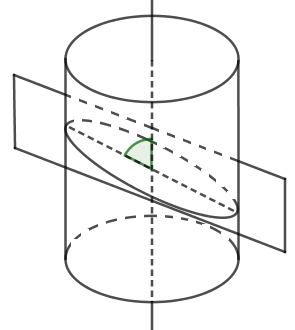
Đáp án cần chọn là: D
</>
Câu 3
A.chiều cao
B.đường kính đáy
C.chu vi đáy
D.bán kính đáy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.10cm3
B.20cm3
C.30cm3
D.40cm3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[10\pi c{m^2}\]
B. \[5\pi c{m^2}\]
C. \[40\pi c{m^2}\]
D. \[20\pi c{m^2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\pi {a^3}\sqrt 3 \]
B. \[\pi {a^3}\]
C. \[\frac{{\pi {a^3}\sqrt 3 }}{4}\]
D. \[3\pi {a^3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\(24\pi \)
B. \(40\pi \)
C. \(18\pi \)
D. \(12\pi \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.