Bài tập Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án
89 người thi tuần này 4.6 1.5 K lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
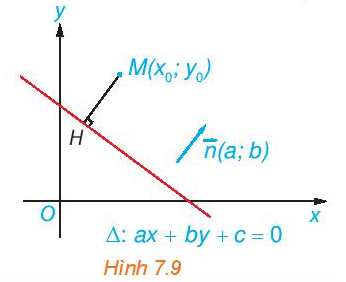
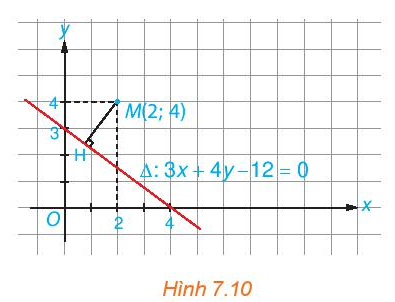
Để biết các yếu tố liên quan tới đường thẳng được thể hiện qua phương trình tương ứng như thế nào ta cùng tìm hiểu qua bài học 20.
Lời giải
Hướng dẫn giải
a) Thay tọa độ điểm M(1; 2) vào phương trình ∆1 ta được:
1 – 2 . 2 + 3 = 0 ⇔ 0 = 0 (luôn đúng).
Do đó điểm M thuộc ∆1.
Thay tọa độ điểm M(1; 2) vào phương trình ∆2 ta được:
3 . 1 – 2 – 1 = 0 ⇔ 0 = 0 (luôn đúng).
Do đó điểm M thuộc ∆2.
Vậy M thuộc cả hai đường thẳng ∆1 và ∆2.
b) Ta có: \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\3x - y - 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x - 2y + 3 = 0\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\6x - 2y - 2 = 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy (2) trừ (1) theo vế ta được: 5x – 5 = 0 ⇔ x = 1.
Thay x = 1 vào (1) ta được: 1 – 2y + 3 = 0 ⇔ 2y = 4 ⇔ y = 2.
Vậy nghiệm của hệ đã cho là (x; y) = (1; 2).
c) Theo câu a, điểm M(1; 2) thuộc cả hai đường thẳng ∆1 và ∆2 nên M là giao điểm của hai đường thẳng này.
Do đó ta thấy tọa độ giao điểm của ∆1 và ∆2 giống với nghiệm của hệ phương trình ở câu b.
Lời giải
Hướng dẫn giải
a) Xét hệ \(\left\{ \begin{array}{l}x + 4y - 3 = 0\,\,\,\,\,\,\left( 1 \right)\\x - 4y - 3 = 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy (1) cộng vế theo vế với (2) ta được: 2x – 6 = 0 ⇔ x = 3.
Thay x = 3 vào (1) ta được: 3 + 4y – 3 = 0 ⇔ 4y = 0 ⇔ y = 0.
Do đó hệ phương trình trên có nghiệm duy nhất (x; y) = (3; 0).
Vậy hai đường thẳng ∆1 và ∆2 cắt nhau tại điểm M(3; 0).
b) Đường thẳng ∆1: x + 2y –\(\sqrt 5 \)= 0 có vectơ pháp tuyến là \({\overrightarrow n _1} = \left( {1;\,\,2} \right)\).
Đường thẳng ∆2: 2x + 4y – \(3\sqrt 5 \) = 0 có vectơ pháp tuyến là \({\overrightarrow n _2} = \left( {2;\,\,4} \right)\).
Ta thấy: \({\overrightarrow n _2} = 2{\overrightarrow n _1}\) nên hai vectơ này cùng phương.
Do đó hai đường thẳng ∆1 và ∆2 song song hoặc trùng nhau.
Mặt khác, ta lại có điểm A(\(\sqrt 5 \); 0) thuộc đường thẳng ∆1 nhưng không thuộc đường thẳng ∆2 nên hai đường thẳng này không trùng nhau.
Vậy hai đường thẳng ∆1 và ∆2 song song với nhau.
Lời giải
Hướng dẫn giải
Hai đường thẳng cắt nhau tạo thành bốn góc, trong đó có hai cặp góc đối đỉnh với nhau. Hai góc đối đỉnh thì có số đo bằng nhau. Một cặp góc đối đỉnh là góc tù thì cặp còn lại là góc nhọn.
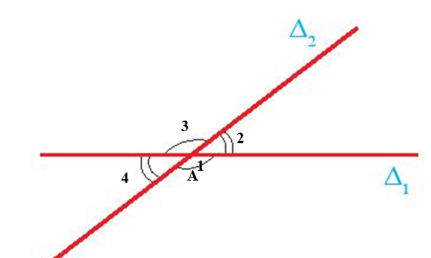
Hai đường thẳng ∆1 và ∆2 cắt nhau tại A như hình trên. Khi đó ta có:
+) \({\widehat A_1} = {\widehat A_3}\) (2 góc đối đỉnh, đây là hai góc tù);
+) \({\widehat A_2} = {\widehat A_4}\) (2 góc đối đỉnh, đây là hai góc nhọn).
Lời giải
Hướng dẫn giải
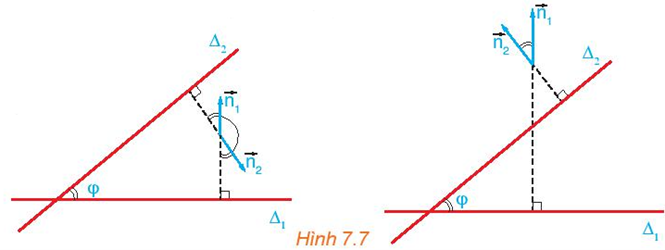
a) Quan sát Hình 7.7, ta thấy góc giữa hai đường thẳng ∆1 và ∆2 là góc φ, góc này bằng hoặc bù với góc giữa hai vectơ \({\overrightarrow n _1}\) và \({\overrightarrow n _2}\).
b)
+) Với trường hợp góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\) bằng nhau thì ta có: cosφ = cos\(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\);
+) Với trường hợp góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\) bù nhau thì ta có: cosφ = – cos\(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.