Giải SBT Toán 9 Chân trời sáng tạo Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác có đáp án
27 người thi tuần này 4.6 275 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
3 bài tập Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng (có lời giải)
6 bài tập Biểu đồ tần số tương đối ghép nhóm dạng cột (có lời giải)
9 bài tập Tần số ghép nhóm, tần số tương đối ghép nhóm (có lời giải)
4 bài tập Biểu đồ tần số tương đối (có lời giải)
Danh sách câu hỏi:
Lời giải
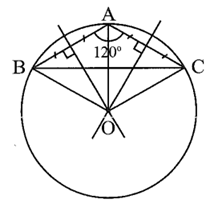
Vẽ đường trung trực của đoạn thẳng AB và AC cắt nhau tại điểm O.
Khi đó OA = OB và OA = OC.
Do đó R = OA = OB = OC, suy ra đường tròn (O; R) ngoại tiếp tam giác ABC.
Ta có AB = AC và OB = OC nên OA là đường trung trực của đoạn thẳng BC.
Vì tam giác ABC cân tại A nên đường trung trực OA của tam giác cũng là tia phân giác của góc BAC, suy ra \(\widehat {OAB} = \frac{1}{2}\widehat {BAC} = \frac{1}{2} \cdot 120^\circ = 60^\circ .\)
Xét ∆OAB cân tại O (OA = OB) có \(\widehat {OAB} = 60^\circ \) nên tam giác OAB là tam giác đều.
Vậy R = OA = AB = 12 (cm).
Lời giải
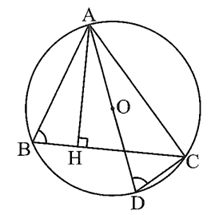
Do AH là đường cao tam giác ABC nên AH ⊥ BC, suy ra \[\widehat {AHB} = \widehat {AHC} = 90^\circ \]
Ta có \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn (O) đường kính AD nên \(\widehat {ACD} = 90^\circ .\)
Xét ∆AHB và ∆ACD có:
\(\widehat {AHB} = \widehat {ACD} = 90^\circ ;\)
\(\widehat {ABH} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC của đường tròn (O)).
Do đó ∆AHB ᔕ ∆ACD (g.g).
Suy ra \(\frac{{AB}}{{AD}} = \frac{{AH}}{{AC}}\) hay AB.AC = AH.AD.
Lời giải
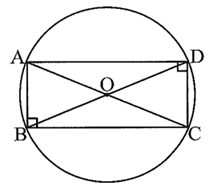
Vì ABCD là hình chữ nhật nên hai tam giác vuông ABC và ADC có chung cạnh huyền AC, do đó chúng cùng có đường tròn ngoại tiếp là (O; R) với tâm O là trung điểm của AC và bán kính bằng \[R = \frac{{AC}}{2}\,.\]
Áp dụng định lí Pythagore cho ∆ABC vuông tại B, ta có:
AC2 = AB2 + BC2 = 52 + 122 = 169.
Suy ra \[AC = \sqrt {169} = 13\] (cm).
Do đó \[R = \frac{{AC}}{2}\,\, = \frac{{13}}{2} = 6,5\;\] (cm).
Lời giải
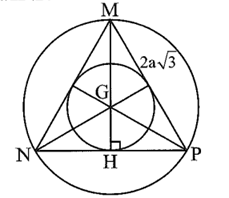
Gọi G là trọng tâm, MH là đường cao của tam giác đều MNP.
Khi đó, đường tròn (G; GM) là đường tròn ngoại tiếp tam giác đều MNP; đường tròn (G; GH) là đường tròn nội tiếp tam giác đều MNP.
Xét ∆MNP đều có MH là đường cao nên đồng thời là đường trung tuyến, hay H là trung điểm của NP, do đó \[NH = PH = \frac{1}{2}NP = \frac{1}{2} \cdot 2a\sqrt 3 = a\sqrt 3 .\]
Xét ∆MNH vuông tại H, theo định lí Pythagore, ta có:
MN2 = MH2 + NH2
Suy ra \(M{H^2} = M{N^2} - N{H^2} = {\left( {2a\sqrt 3 } \right)^2} - {\left( {a\sqrt 3 } \right)^2} = 3a.\)
Do đó \(MG = \frac{2}{3}MH = \frac{2}{3} \cdot 3a = 2a;\,\,GH = \frac{1}{3}MH = \frac{1}{3} \cdot 3a = a.\)
Vậy bán kính các đường tròn ngoại tiếp và nội tiếp tam giác MNP lần lượt là 2a và a.
Lời giải
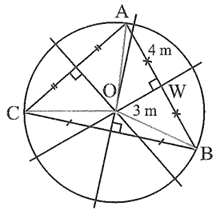
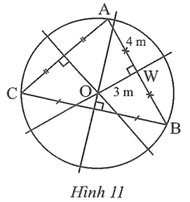
Điểm O cách đều 3 điểm A, B, C nên O là tâm của đường tròn ngoại tiếp tam giác ABC.
Suy ra O là giao điểm của 3 đường trung trực của tam giác ABC.
Trong tam giác OWA vuông tại W, theo định lí Pythagore, ta có:
OA2 = OW2 + WA2 = 32 + 42 = 25.
Suy ra \[OA = \sqrt {25} = 5\;({\rm{m}}).\]
Vậy khoảng cách từ mỗi quầy hàng đến điểm đặt thùng rác là 5 m.