Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20cm, tạo thành bốn tam giác xung quanh như hình vẽ.
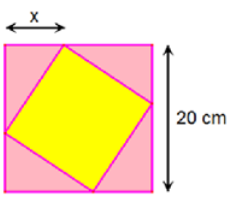
Tìm tập hợp các giá trị của x để diện tích viên gạch không vượt quá 208cm2.
A.\[8 \le x \le 12\]
B. \[6 \le x \le 14\]
C. \[12 \le x \le 14\]
D. \[12 \le x \le 18\]
Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bất phương trình !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
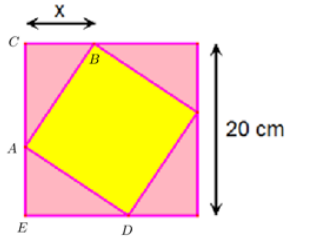
Ta có:\[\angle CAB + \angle BAD + \angle DAE = {180^o}\]
\[ \Rightarrow \angle CAB + \angle EAD = {90^o}\]
Mà \[\angle CAB + \angle CBA = {90^o}\] (\[\Delta CAB\]vuông tại C)
\[ \Rightarrow \angle CBA = \angle EAD\] kết hợp\[AB = AD\,\,\,\left( {gt} \right)\]
\[\begin{array}{*{20}{l}}{ \Rightarrow {\rm{\Delta }}CAB = {\rm{\Delta }}EDA\,\,\,\left( {ch - gn} \right)}\\{ \Rightarrow CB = EA = x \Rightarrow CA = CE - EA = 20 - x\,\,\,\,\left( {cm} \right)}\end{array}\]
Diện tích viên gạch là\[S = A{B^2} = C{B^2} + C{A^2} = {x^2} + {\left( {20 - x} \right)^2}\]
Vì \[S \le 208 \Leftrightarrow {x^2} + {\left( {20 - x} \right)^2} \le 208 \Leftrightarrow 2{x^2} - 40x + 192 \le 0 \Leftrightarrow 8 \le x \le 12\]
Đáp án cần chọn là: A
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Điều kiện\[x \ge - 7\]
Đặt \[t = \sqrt {x + 7} \] điều kiện \[t \ge 0\]
Ta có\[\sqrt {{t^2} + 1 - 2t} = 2 - \sqrt {{t^2} - 6 - t} \Leftrightarrow \left| {t - 1} \right| = 2 - \sqrt {{t^2} - t - 6} \]
Nếu \[t \ge 1\] thì ta có\[3 - t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 9 - 6t + {t^2}}\\{t \le 3}\end{array}} \right. \Leftrightarrow t = 3 \Leftrightarrow \sqrt {x + 7} = 3 \Leftrightarrow x = 2\]
Nếu t < 1 thì ta có \[1 + t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 1 + 2t + {t^2}}\\{t \ge - 1}\end{array}} \right. \Leftrightarrow t = - \frac{7}{3}\;\;\left( l \right)\]
Đáp án cần chọn là: B
</>
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số nguyên lớn nhất bạn An có thể chọn là \[x\left( {x \in \mathbb{Z}} \right)\]
Theo bài ra ta có \[2\left( {4x - 30} \right) - 10\] là số có 2 chữ số.
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{10 \le 2(4x - 30) - 10 \le 99}\\{ - 99 \le 2(4x - 30) - 10 \le - 10}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{20 \le 2(4x - 30) \le 109}\\{ - 89 \le 2(4x - 30) \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{10 \le 4x - 30 \le \frac{{109}}{2}}\\{ - \frac{{89}}{2} \le 4x - 30 \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{40 \le 4x \le \frac{{169}}{2}}\\{ - \frac{{29}}{2} \le 4x \le 30}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{10 \le x \le \frac{{169}}{8}}\\{ - \frac{{29}}{8} \le x \le \frac{{30}}{4}}\end{array}} \right.\)
Vì \[x \in \mathbb{Z}\] và x là số lớn nhất nên x=21.
Vậy số lớn nhất An có thể chọn có hàng đơn vị bằng 1.
Đáp án cần chọn là: C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.a=1.
B.\[a \in \left( {1;10} \right)\]
C. \[a \in \left[ {4;\frac{{45}}{4}} \right]\]
D. \[a \in \left( {4;\frac{{43}}{4}} \right)\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[3 < x \le 5\]
B. \[2 < x \le 3\]
C. \[ - 5 < x \le - 3\]
D. \[ - 3 < x \le - 2\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập
10 - Đinh Ngọc Hậu lớp 8.4 -
tại sao lại ra 192 ngay 920-x)^2