Câu hỏi:

29/06/2022 275

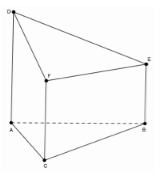
Cho hình lăng trụ xiên ABC.A′B′C′ có đáy ABC là tam giác đều với tâm O. Hình chiếu của C′ trên (ABC) là O. Tính thể tích của lăng trụ biết rằng khoảng cách từ O đến CC′ là a và 2 mặt bên (ACC′A′) và (BCC′B′) hợp với nhau góc 90⁰.

A.\[\frac{{{a^3}\sqrt 2 }}{4}\]

B. \[\frac{{3{a^3}\sqrt 2 }}{8}\]

C. \[\frac{{9{a^3}\sqrt 2 }}{8}\]

D. \[\frac{{27{a^3}\sqrt 2 }}{8}\]

Xem lời giải

Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Thể tích khối hộp !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

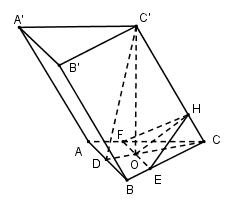
Gọi D là trung điểm của AB. Trong (CC′D) kẻ \[OH \bot CC' \Rightarrow OH = a\]

\(\left. {\begin{array}{*{20}{c}}{CD \bot AB}\\{C\prime O \bot AB}\end{array}} \right\} \Rightarrow AB \bot (CC\prime D) \Rightarrow AB \bot CC\prime \)

Trong (ABC), qua O kẻ\[EF//AB\left( {E \in BC;F \in AC} \right)\]

Ta có: \(\left. {\begin{array}{*{20}{c}}{EF \bot CC\prime }\\{OH \bot CC'}\end{array}} \right\} \Rightarrow CC\prime \bot (EFH) \Rightarrow CC\prime \bot HE;CC\prime \bot HF\)

Ta có:

\(\left. {\begin{array}{*{20}{c}}{(ACC\prime A\prime ) \cap (BCC\prime B\prime ) = CC\prime }\\{(ACC\prime A\prime ) \supset HF \bot CC\prime }\\{(BCC\prime B\prime ) \supset HE \bot CC\prime }\end{array}} \right\} \Rightarrow ((ACC\prime \widehat {A\prime );(B}CC\prime B\prime )) = (H\widehat {F;H}E) = {90^0}\)

\[ \Rightarrow HE \bot HF\]

\[ \Rightarrow {\rm{\Delta }}HEF\] vuông tại H

\[{\rm{\Delta }}HCE = {\rm{\Delta }}HCF\left( {c.g.v - c.h} \right) \Rightarrow HE = HF \Rightarrow {\rm{\Delta }}HEF\] vuông cân tại H\[ \Rightarrow EF = 2HO = 2a\]

Ta có:\[\frac{{EF}}{{AB}} = \frac{{CO}}{{CD}} = \frac{2}{3} \Rightarrow AB = \frac{3}{2}EF = \frac{3}{2}.2a = 3a\]

\[ \Rightarrow {S_{{\rm{\Delta }}ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{9{a^2}\sqrt 3 }}{4}\]

\[CD = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{2} \Rightarrow CO = \frac{2}{3}AB = \frac{2}{3}.\frac{{3a\sqrt 3 }}{2} = a\sqrt 3 \]

\[C'O \bot \left( {ABC} \right) \Rightarrow C'O \bot CO \Rightarrow {\rm{\Delta }}CC'O\] vuông tại O

\[ \Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{{C'{O^2}}} + \frac{1}{{C{O^2}}} \Rightarrow \frac{1}{{C'{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{C{O^2}}} = \frac{1}{{{a^2}}} - \frac{1}{{3{a^2}}} = \frac{2}{{3{a^2}}} \Rightarrow C'O = \frac{{\sqrt 6 }}{2}a\]

Vậy\[{V_{ABC.A'B'C'}} = C'O.{S_{{\rm{\Delta }}ABC}} = \frac{{a\sqrt 6 }}{2}.\frac{{9{a^2}\sqrt 3 }}{4} = \frac{{27{a^3}\sqrt 2 }}{8}\]

Đáp án cần chọn là: D

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:

A.75

B.36

C.18

D.54

Lời giải

Cạnh của khối lập phương đã cho là:\[a = \sqrt[3]{{27}} = 3.\]

⇒ Diện tích toàn phần của khối lập phương đã cho là:\[{6.3^2} = 54.\]

Đáp án cần chọn là: D

Câu 2

Cho đa diện ABCDEF có AD,BE,CF đôi một song song. AD⊥(ABC), AD+BE+CF=5, diện tích tam giác ABC bằng 10. Thể tích đa diện ABCDEF bằng

A.50

B. \[\frac{{15}}{2}\]

C. \[\frac{{50}}{3}\]

D. \[\frac{{15}}{4}\]

Lời giải

Chọn\[AD = BE = CF = \frac{5}{3}\] thì đa diện là hình lăng trụ đứng\[ABC.DEF\] có diện tích đáy\[{S_{ABC}} = 10\] và chiều cao\[AD = \frac{5}{3}\]

Thể tích\[V = {S_{ABC}}.AD = 10.\frac{5}{3} = \frac{{50}}{3}\]

Đáp án cần chọn là: C

Câu 3

Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích V. Trên đáy A′B′C′ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:

A.\[\frac{V}{2}\]

B. \[\frac{{2V}}{3}\]

C. \[\frac{V}{3}\]

D. \[\frac{{3V}}{4}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình lăng trụ ABC.A′B′C′ có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C trên (ABB′A′) là tâm của hình bình hành ABB′A′. Thể tích của khối lăng trụ là:

A.\[\frac{{{a^3}}}{4}\]

B. \[\frac{{{a^3}\sqrt 2 }}{2}\]

C. \[\frac{{{a^3}\sqrt 2 }}{4}\]

D. \[\frac{{{a^3}}}{2}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho lăng trụ đứng ABC.A′B′C′ với ABC là tam giác vuông cân tại C có AB=a , mặt bên ABB′A′ là hình vuông. Mặt phẳng qua trung điểm I của AB và vuông góc với AB′ chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?

A.\[{V_1} = \frac{{{a^3}}}{{48}},{V_2} = \frac{{11{a^3}}}{{24}}\]

B. \[{V_1} = \frac{{{a^3}}}{{24}},{V_2} = \frac{{11{a^3}}}{{48}}\]

C. \[{V_1} = \frac{{{a^3}}}{{48}},{V_2} = \frac{{11{a^3}}}{{48}}\]

D. \[{V_1} = \frac{{{a^3}}}{{24}},{V_2} = \frac{{5{a^3}}}{{24}}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho khối lăng trụ tam giác ABC.A′B′C′ mà mặt bên ABB′A′ có diện tích bằng 4. Khoảng cách giữa CC′ và mặt phẳng (ABB′A′) bằng 7. Thể tích khối lăng trụ là:

A.10

B.12

C.14

D.16

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy ABC một góc 60⁰. Thể tích khối lăng trụ là:

A.\[\frac{{3{a^3}\sqrt 3 }}{8}\]

B. \[\frac{{{a^3}\sqrt 3 }}{8}\]

C. \[\frac{{3{a^3}}}{8}\]

d. \[\frac{{{a^3}}}{8}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:

Cho đa diện ABCDEF có AD,BE,CF đôi một song song. AD⊥(ABC), AD+BE+CF=5, diện tích tam giác ABC bằng 10. Thể tích đa diện ABCDEF bằng

Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích V. Trên đáy A′B′C′ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:

Cho hình lăng trụ ABC.A′B′C′ có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C trên (ABB′A′) là tâm của hình bình hành ABB′A′. Thể tích của khối lăng trụ là:

Cho lăng trụ đứng ABC.A′B′C′ với ABC là tam giác vuông cân tại C có AB=a , mặt bên ABB′A′ là hình vuông. Mặt phẳng qua trung điểm I của AB và vuông góc với AB′ chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?

Cho khối lăng trụ tam giác ABC.A′B′C′ mà mặt bên ABB′A′ có diện tích bằng 4. Khoảng cách giữa CC′ và mặt phẳng (ABB′A′) bằng 7. Thể tích khối lăng trụ là:

Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy ABC một góc 600. Thể tích khối lăng trụ là:

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy ABC một góc 60⁰. Thể tích khối lăng trụ là: