Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD,BC; AD = 3BC = 3a, AB = a,\(SA = a\sqrt 3 \). Điểm I thỏa mãn \(\overrightarrow {AD} = 3\overrightarrow {AI} \); M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng(ABCD).
A.\[V = \frac{{\pi {a^3}}}{{2\sqrt 5 }}\]
B. \[V = \frac{{\pi {a^3}}}{{\sqrt 5 }}\]
C. \[V = \frac{{\pi {a^3}}}{{10\sqrt 5 }}\]
D. \[V = \frac{{\pi {a^3}}}{{5\sqrt 5 }}\]
Quảng cáo
Trả lời:
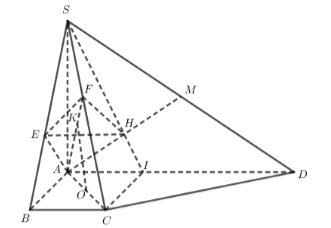
Xét tam giác SAD vuông tại A có \[SA = a\sqrt 3 ,AD = 3a \Rightarrow \widehat {SDA} = {30^0} \Rightarrow \widehat {MAI} = {30^0}\]
Lại có tam giác SAI vuông tại A có\[SA = a\sqrt 3 ,AI = a \Rightarrow \widehat {SIA} = {60^0}\] nên tam giác AHI có\[\hat H = {90^0}\] hay \[AH \bot SI\]
Mà \[AH \bot IC\] do \[IC//BA \bot \left( {SAD} \right)\] nên \[AH \bot \left( {SIC} \right) \Rightarrow AH \bot SC\]Ngoài ra,\[AE \bot SB,AE \bot BC\left( {BC \bot \left( {SAB} \right)} \right) \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC\]
Mà\[AF \bot SC\] nên\[SC \bot \left( {AEFH} \right)\] và AEFH là tứ giác có \[\hat E = \hat H = {90^0}\] nên nội tiếp đường tròn tâm K là trung điểm AF đường kính AF.Gọi O là trung điểm AC thì OK//SC, mà\[SC \bot \left( {AEFH} \right)\] nên \[OK \bot \left( {AEFH} \right)\] hay O chính là đỉnh hình nón và đường tròn đáy là đường tròn đường kính AF.
Ta tính AF,OK.
Xét tam giác SAC vuông tại A đường cao AF nên
\[AF = \frac{{SA.AC}}{{SC}} = \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{a\sqrt 6 }}{{\sqrt 5 }};OK = \frac{1}{2}CF = \frac{1}{2}.\frac{{C{A^2}}}{{CS}} = \frac{a}{{\sqrt 5 }}\]
Vậy thể tích \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .\frac{a}{{\sqrt 5 }}.{\left( {\frac{1}{2}.\frac{{a\sqrt 6 }}{{\sqrt 5 }}} \right)^2} = \frac{{\pi {a^3}}}{{10\sqrt 5 }}\]
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{{7\pi }}{3}\]
B. \[\frac{{7\pi }}{6}\]
C. \[\frac{{14\pi }}{3}\]
D. \[\frac{{14\pi }}{9}\]
Lời giải
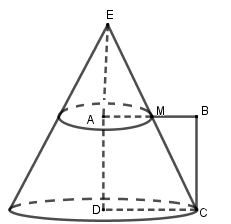
Kéo dài CM cắt DA tại E. Quay hình thang vuông AMCD quanh trục AD ta được hình nón cụt như hình vẽ.
Quay tam giác EDC quanh trục ED ta được hình nón.
Dễ thấy \[{V_{nc}} = {V_1} - {V_2}\] V1V1 là thể tích khối nón đỉnh E, bán kính đáy DC = 2DC = 2 và V2 là thể tích khối nón đỉnh E, bán kính đáy AM = 1
Có\[\frac{{EA}}{{ED}} = \frac{{AM}}{{DC}} = \frac{1}{2} \Rightarrow EA = AD = 2 \Rightarrow ED = 4\]
\[ \Rightarrow {V_1} = \frac{1}{3}\pi D{C^2}.ED = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\]
\[{V_2} = \frac{1}{3}\pi A{M^2}EA = \frac{1}{3}\pi {.1^2}.2 = \frac{{2\pi }}{3}\]
Vậy \[V = {V_1} - {V_2} = \frac{{16\pi }}{3} - \frac{{2\pi }}{3} = \frac{{14\pi }}{3}\]
Đáp án cần chọn là: C
Câu 2
A.AB,OA
B.AB,OB
C.OA,OB
D. OB,OA
Lời giải
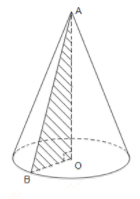
Quan sát hình vẽ ta thấy đường sinh là AB và đường cao AO.
Đáp án cần chọn là: A
Câu 3
A.\[{S_{xq}} = \frac{1}{3}\pi rl\]
B. \[{S_{xq}} = \pi {r^2}l\]
C. \[{S_{xq}} = \pi rl + \pi {r^2}\]
D. \[{S_{xq}} = \pi rl\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[\frac{h}{r} = 3\]
B. \[\frac{h}{r} = 2\]
C. \[\frac{h}{r} = \frac{4}{3}\]
D. \[\frac{h}{r} = \frac{{16}}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[h = R\sqrt 3 \]
B. \[h = R\sqrt 2 \]
C. \[h = \frac{{4R}}{3}\]
D. \[h = \frac{{2R}}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[l = \frac{{r.{S_{xq}}}}{\pi }\]
B. \[l = \frac{{{S_{xq}}}}{{2\pi r}}\]
C. \[l = \frac{{{S_{xq}}}}{{\pi r}}\]
D. \[l = \frac{{3{S_{xq}}}}{{\pi r}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.