Cho điểm A(0;8;2) và mặt cầu (S) có phương trình \[\left( S \right):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72\;\]và điểm B(1;1;−9). Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử \[\overrightarrow n = \left( {1;m;n} \right)\;\]là véctơ pháp tuyến của (P). Lúc đó:
A.\[mn = \frac{{276}}{{49}}\]
B. \[mn = - \frac{{276}}{{49}}\]
C. \[mn = 4\]
D. \[mn = - 4\]
Quảng cáo
Trả lời:
(S) có tâm I(5;−3;7) và bán kính\[R = 6\sqrt 2 \]
Theo đề bài ta có phương trình (P) có dạng\[x + m(y - 8) + n(z - 2) = 0\]
Vì (P) tiếp xúc với (S) nên
\[{\rm{d}}(I,(P)) = \frac{{\left| {5 + m( - 3 - 8) + n(7 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \frac{{\left| {5 - 11m + 5n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 6\sqrt 2 \]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow \left| {5 - 11m + 5n} \right| = 6\sqrt 2 .\sqrt {1 + {m^2} + {n^2}} }\\{ \Leftrightarrow 25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn = 72(1 + {m^2} + {n^2})}\\{ \Leftrightarrow 49{m^2} - 110m + 50n - 110mn - 47{n^2} - 47 = 0}\\{ \Leftrightarrow 49{m^2} - 110m(n + 1) - 47{n^2} + 50n - 47 = 0(1)}\\{{\rm{\Delta '}} = 3025{{(n + 1)}^2} - 49( - 47{n^2} + 50n - 47) = 5328{n^2} + 3600n + 5328 > 0}\end{array}\]
Phương trình (*) luôn có nghiệm
\[\begin{array}{*{20}{l}}{{\rm{d}}(B,(P)) = \frac{{\left| {1 + m(1 - 8) + n( - 9 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \frac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }}}\\{ = > d(B,(P))\max = AB \Leftrightarrow \frac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 3\sqrt {19} \Leftrightarrow \sqrt {1 + {m^2} + {n^2}} = \frac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }}}\end{array}\]
Mặt khác\[\frac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }} = \sqrt {1 + {m^2} + {n^2}} \]
\[\frac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }} = \frac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }}\]
\[\begin{array}{*{20}{l}}{72(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 171(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)}\\{ \Leftrightarrow 8(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 19(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)}\\{ \Leftrightarrow - 1907{m^2} + 493{n^2} + 1978m - 1126n + 3322mn - 467 = 0(2)}\end{array}\]Từ (1) và (2)\[ \Rightarrow m.n = \frac{{276}}{{49}}\]
Đáp án cần chọn là: A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 2\]
B. \[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 3\]
C. \[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 4\]
D. \[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9\]Trả lời:
Lời giải
Khoảng cách từ I đến (P) được tính theo công thức
\[d\left( {I;\left( P \right)} \right) = \frac{{\left| {2.\left( { - 1} \right) - 2 - 2.3 + 1} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = 3\]
Phương trình mặt cầu cần tìm là \[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9\]
Đáp án cần chọn là: D
Câu 2
A.\[\left( { - \frac{7}{3}; - \frac{7}{3}; - \frac{2}{3}} \right)\]
B. \[\left( { - 2; - 2; - 2} \right)\]
C. \[\left( { - \frac{2}{3}; - \frac{7}{3}; - \frac{7}{3}} \right)\]
D. \[\left( { - \frac{7}{3}; - \frac{2}{3}; - \frac{7}{3}} \right)\]
Lời giải
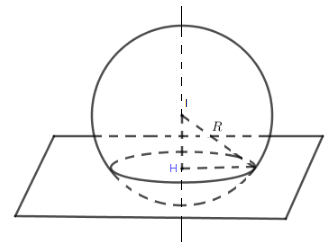
(S) có tâm I(1;1;1) và bán kính R=8.
Tâm đường tròn giao tuyến (C) là hình chiếu vuông góc H của I trên (P).
Đường thẳng \[\Delta \] qua I và vuông góc với (P) có phương trình là
\[\frac{{x - 1}}{2} = \frac{{y - 1}}{2} = \frac{{z - 1}}{1}\]
Do\[H \in \Delta \] nên\[H(2t + 1;2t + 1;t + 1)\]
Ta có\[H \in (P)\] nên:
\[2(2t + 1) + 2(2t + 1) + t + 1 + 10 = 0 \Leftrightarrow 9t + 15 = 0 \Leftrightarrow t = - \frac{5}{3}\]
\( \Rightarrow H(\frac{{ - 7}}{3};\frac{{ - 7}}{3};\frac{{ - 2}}{3})\)
Đáp án cần chọn là: A
Câu 3
A.\[{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 18\]
B. \[{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = 4\]
C. \[{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = 18\]
D. \[{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 4\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[x + y - 3z - 8 = 0\]
B. \[x - y - 3z + 3 = 0\]
C. \[x + y + 3z - 9 = 0\]
D. \[x + y - 3z + 3 = 0\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[{\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 2\]
B. \[{\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 9\]
C. \[{\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 4\]
D. \[{\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 16\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.2
B. \[\frac{2}{3}\]
C. \[\frac{2}{9}\]
D. \[\frac{4}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[x - 2y + 3z - 2 = 0\]
B. \[x - 2y - 3z - 2 = 0\]
C. \[x + 2y - 3z - 6 = 0\]
D. \[2x - y - 1 = 0\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.