Tìm điểm A cố định mà họ đồ thị hàm số \[y = {x^2} + (2 - m)x + 3m\,\,\,\,\,\,\,\,\,\,({P_m})\;\] luôn đi qua.
A.A(3;15)
B.A(0;−2)
C.A(3;−15)
D.A(−3;−15)
Quảng cáo
Trả lời:
Điểm\[A\left( {{x_0};\,\,{y_0}} \right)\] là điểm cố định của họ (Pm) khi và chỉ khi
\[{y_0} = {x_0}^2 + (2 - m){x_0} + 3m \Leftrightarrow x_0^2 + 2{x_0} - {y_0} - m({x_0} - 3) = 0,\forall m\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x_0^2 + 2{x_0} - {y_0} = 0}\\{{x_0} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_0} = 3}\\{{y_0} = 15}\end{array}} \right.\)
Suy ra A(3;15).
Đáp án cần chọn là: A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bước 1:
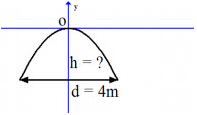
Gọi hai điểm chân cổng là \[A\left( {{x_A};{y_A}} \right)\] và \[B\left( {{x_B};{y_B}} \right)\] thì ta có \[{y_A} = {y_B}\] và \[\left| {{x_A}} \right| = \left| {{x_B}} \right|.\]
Vì d = 4 nên \[\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2.\]
Bước 2: Tính h
Vậy \[h = \left| {{y_A}} \right| = \left| { - \frac{1}{2}x_A^2} \right| = \left| { - \frac{1}{2}{{.2}^2}} \right| = 2\,\left( m \right).\]
Câu 2
A.\(\left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 2}\end{array}} \right.\)
B. \(\left[ {\begin{array}{*{20}{c}}{m < 1}\\{m >2}\end{array}} \right.\)
C. 1 < m < 2
D. Không xác định được
Lời giải
Xét phương trình hoành độ giao điểm \[{x^2} - 2x + m - 1 = 0\,\,\left( * \right)\]
Để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương thì phương trình (*) có 2 nghiệm dương phân biệt.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta \prime >0}\\{S >0}\\{P >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 - m + 1 >0}\\{2 >0}\\{m - 1 >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m < 2}\\{m >1}\end{array}} \right. \Leftrightarrow 1 < m < 2\)
Đáp án cần chọn là: C
Câu 3
A.\[y = \frac{1}{{18}}{x^2} + \frac{1}{6}x - 5\]
B. \[y = \frac{1}{{18}}{x^2} + \frac{1}{6}x + 5\]
C. \[y = 3{x^2} + 9x - 9\]
D. \[y = - \frac{1}{{18}}{x^2} + \frac{1}{6}x - 5\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[y = {x^2} - 6x + 3\]
B. \[y = - \frac{5}{9}{x^2} + \frac{{10}}{3}x + 3\]
C. \[y = 3{x^2} + 9x + 3\]
D. \[y = \frac{5}{9}{x^2} - \frac{{10}}{3}x + 3\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.m >0
B. m < 0
C. m = 0
D.Không xác định được
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[y = - 5{x^2} + 8x + 2\]
B. \[y = 10{x^2} + 13x + 2\]
C. \[y = - 10{x^2} - 13x + 2\]
D. \[y = 9{x^2} + 6x - 5\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
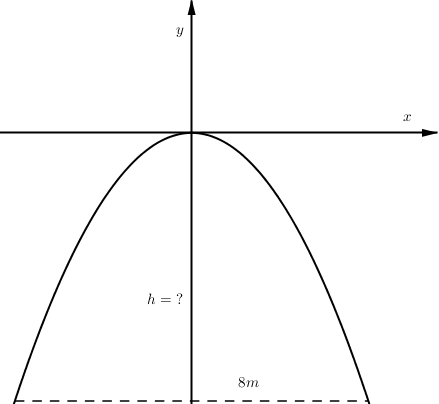
Câu 7
A. h = 8m.
B. h = 7m.
C. h = 9m.
D. h = 5m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.