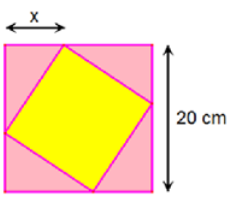
Cho bất phương trình: \[{x^2} - 2x \le \left| {x - 2} \right| + ax - 6\]. Giá trị dương nhỏ nhất của a để bất phương trình có nghiệm gần nhất với số nào sau đây:
A.0,5.
B.1,6.
C.2,2.
D.2,6.
Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bất phương trình !!
Quảng cáo
Trả lời:
Trường hợp 1:\[x \in \left[ {2; + \infty } \right)\]
Khi đó bất phương trình đã cho trở thành:
\[{x^2} - \left( {a + 3} \right)x + 8 \le 0 \Leftrightarrow a \ge x + \frac{8}{x} - 3 \ge 4\sqrt 2 - 3 \approx 2,65\forall x \in \left[ {2; + \infty } \right)\]
Dấu xảy ra khi\[x = 2\sqrt 2 \]
Trường hợp 2:\[x \in \left( { - \infty ;2} \right)\]
Khi đó bất phương trình đã cho trở thành:
\[{x^2} - \left( {a + 1} \right)x + 4 \le 0\]
\[ \Leftrightarrow ax \ge {x^2} - x + 4\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a \ge \frac{{{x^2} - x + 4}}{x}\,\,khi\,\,x \in (0;2)}\\{a \le \frac{{{x^2} - x + 4}}{x}\,\,\,\,khi\,x \in ( - \infty ;0)}\end{array}} \right.\,\,\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a \ge x + \frac{4}{x} - 1\,\,\,khi\,\,\,x \in (0;2)\,\,\,\,\,(1)}\\{a \le x + \frac{4}{x} - 1\,\,\,khi\,\,\,x \in ( - \infty ;0)\,\,\,\,\,(2)}\end{array}} \right.\)
Giải (1) ta được a >3 (theo bất đẳng thức Cauchy).
Giải (2): \[a \le x + \frac{4}{x} - 1 \Leftrightarrow a \le - 2\sqrt {x.\frac{4}{x}} - 1 = - 5\]
Vậy giá trị dương nhỏ nhất của a gần với số 2,6.
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[8 \le x \le 12\]
B. \[6 \le x \le 14\]
C. \[12 \le x \le 14\]
D. \[12 \le x \le 18\]
Lời giải
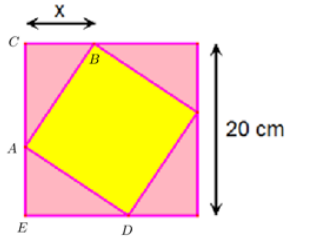
Ta có:\[\angle CAB + \angle BAD + \angle DAE = {180^o}\]
\[ \Rightarrow \angle CAB + \angle EAD = {90^o}\]
Mà \[\angle CAB + \angle CBA = {90^o}\] (\[\Delta CAB\]vuông tại C)
\[ \Rightarrow \angle CBA = \angle EAD\] kết hợp\[AB = AD\,\,\,\left( {gt} \right)\]
\[\begin{array}{*{20}{l}}{ \Rightarrow {\rm{\Delta }}CAB = {\rm{\Delta }}EDA\,\,\,\left( {ch - gn} \right)}\\{ \Rightarrow CB = EA = x \Rightarrow CA = CE - EA = 20 - x\,\,\,\,\left( {cm} \right)}\end{array}\]
Diện tích viên gạch là\[S = A{B^2} = C{B^2} + C{A^2} = {x^2} + {\left( {20 - x} \right)^2}\]
Vì \[S \le 208 \Leftrightarrow {x^2} + {\left( {20 - x} \right)^2} \le 208 \Leftrightarrow 2{x^2} - 40x + 192 \le 0 \Leftrightarrow 8 \le x \le 12\]
Đáp án cần chọn là: A
Lời giải
Điều kiện\[x \ge - 7\]
Đặt \[t = \sqrt {x + 7} \] điều kiện \[t \ge 0\]
Ta có\[\sqrt {{t^2} + 1 - 2t} = 2 - \sqrt {{t^2} - 6 - t} \Leftrightarrow \left| {t - 1} \right| = 2 - \sqrt {{t^2} - t - 6} \]
Nếu \[t \ge 1\] thì ta có\[3 - t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 9 - 6t + {t^2}}\\{t \le 3}\end{array}} \right. \Leftrightarrow t = 3 \Leftrightarrow \sqrt {x + 7} = 3 \Leftrightarrow x = 2\]
Nếu t < 1 thì ta có \[1 + t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 1 + 2t + {t^2}}\\{t \ge - 1}\end{array}} \right. \Leftrightarrow t = - \frac{7}{3}\;\;\left( l \right)\]
Đáp án cần chọn là: B
</>
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[3 < x \le 5\]
B. \[2 < x \le 3\]
C. \[ - 5 < x \le - 3\]
D. \[ - 3 < x \le - 2\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.a=1.
B.\[a \in \left( {1;10} \right)\]
C. \[a \in \left[ {4;\frac{{45}}{4}} \right]\]
D. \[a \in \left( {4;\frac{{43}}{4}} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.