Câu hỏi:

23/05/2022 231

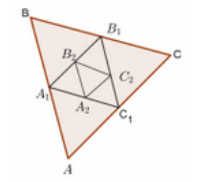
Cho tam giác đều ABC cạnh a. Tam giác \[{A_1}{B_1}{C_1}\] có đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \[{A_2}{B_2}{C_2}\] có các đỉnh là trung điểm các cạnh của tam giác \[{A_1}{B_1}{C_1}\],…, tam giác AnBnCnAnBnCn có các đỉnh là trung điểm các cạnh của tam giác \[{A_{n - 1}}{B_{n - 1}}{C_{n - 1}} \ldots .{\rm{ }}Goi\;P,{P_1},{P_2},...,{P_n},...\] là chu vi của các tam giác \[ABC,{A_1}{B_1}{C_1},{A_2}{B_2}{C_2},...,{A_n}{B_n}{C_n},...\] Tìm tổng \[P,{P_1},{P_2},...,{P_n},...\]

A.9a

B.6a

C.\[ + \infty \]

D.3a

Xem lời giải

Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Giới hạn của dãy số !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Bước 1:

Gọi \[{a_n}\] là cạnh của tam giác \[{A_n}{B_n}{C_n}\] với n nguyên dương.

Ta cần chứng minh cạnh của tam giác bất kì \[{A_n}{B_n}{C_n}\] bằng\[{a_n} = \frac{a}{{{2^n}}}\] ới mọi số nguyên dương n (*)

Vì\[{A_1},{B_1},{C_1}\] là trung điểm các cạnh của tam giác ABC nên \[{a_1} = \frac{a}{2}\]

Cạnh của tam giác\[{A_1}{B_1}{C_1}\] có cạnh là\[\frac{a}{2} = \frac{a}{{{2^1}}}\]

Giả sử (*) đúng với \[n = k\]

Tức là cạnh của tam giác\[{A_k}{B_k}{C_k}\] là\[{a_k} = \frac{a}{{{2^k}}}\]

Ta có\[{A_{k + 1}}{B_{k + 1}}{C_{k + 1}}\] có cạnh bằng một nửa cạnh của tam giác\[{A_k}{B_k}{C_k}\] nên có cạnh là\[{a_{k + 1}} = \frac{{{a_k}}}{2} = \frac{1}{2}.\frac{a}{{{2^k}}} = \frac{a}{{{2^{k + 1}}}}\]

=>(*) đúng với \[n = k + 1\]

=>(*) đúng với mọi số nguyên dương n.

=>Chu vi của tam giác\[{A_n}{B_n}{C_n}\] như giả thiết là\[{P_n} = \frac{{3a}}{{{2^n}}}\]

Bước 2:

Như vậy\[P = 3a;{P_1} = \frac{{3a}}{2};{P_2} = \frac{{3a}}{{{2^2}}};...;{P_n} = \frac{{3a}}{{{2^n}}};...\]

Dãy số\[\left( {{P_n}} \right)\] gồm\[P,{P_1},{P_2},...\] là cấp số nhân với số hạng đầu là\[P = 3a\] công bội\[q = \frac{1}{2}\]

\[ \Rightarrow P + {P_1} + {P_2} + ... = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\]

Đáp án cần chọn là: B

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính giới hạn \[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\].

A.\[\frac{1}{5}\]

B. $\frac{1}{2}$

C. 0

D. \[\frac{{ - 3}}{2}\]

Lời giải

Bước 1:

\[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}} = \lim \frac{{{n^3}\left( { - 3 + \frac{1}{n}} \right)}}{{{n^3}\left( {2 + \frac{5}{n} - \frac{2}{{{n^3}}}} \right)}}\]

Bước 2:

\[ = \lim \frac{{ - 3 + \frac{1}{n}}}{{2 + \frac{5}{n} - \frac{2}{{{n^3}}}}} = \frac{{ - 3 + 0}}{{2 + 0 - 0}} = \frac{{ - 3}}{2}\]

Đáp án cần chọn là: D

Câu 2

$Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục (ảnh 1)$

Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục như thế, ta được hình vuông \[{A_3}{B_3}{C_3}{D_3}\] có diện tích \[{S_3}, \ldots \;\] Tính tổng \[{S_1} + {S_2} + \ldots \;\] bằng

A.\[\frac{{{a^2}\left( {{2^{100}} - 1} \right)}}{{{2^{100}}}}\]

B. \[2{a^2}\]

C. \[\frac{{{a^2}}}{{{2^{100}}}}\]

D. \[\frac{{{a^2}\left( {{2^{99}} - 1} \right)}}{{{2^{98}}}}\]

Lời giải

Bước 1: Tìm cấp số nhân

Ta có:

\[\begin{array}{l}{{\rm{S}}_1} = {a^2}\\{{\rm{S}}_2} = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = {a^2} \cdot \frac{1}{2}\\{{\rm{S}}_3} = {\left( {\frac{{a\sqrt 2 }}{2} \cdot \frac{{\sqrt 2 }}{2}} \right)^2}\\ \cdots \\{{\rm{S}}_{\rm{n}}} = {a^2} \cdot {\left( {\frac{1}{2}} \right)^{n - 1}}\end{array}\]

Có\[{S_1};{S_2};{S_3}; \ldots \] là một cấp số nhân lùi vô hạn với:

- Số hạng đầu:\[{S_1} = {a^2}\]

- Công bội:\[q = \frac{1}{2}\]

Bước 2: Sử dụng công thức tổng cấp số nhân lùi vô hạn

Do đó:\[S = {S_1} + {S_2} + {S_3} + \ldots = \frac{{{S_1}}}{{1 - q}} = \frac{{{a^2}}}{{1 - \frac{1}{2}}} = 2{a^2}\]

Đáp án cần chọn là: B

Câu 3