Câu hỏi:
27/06/2022 222Tìm m để phương trình \[{4^x} - \;{2^{x\; + \;3}} + \;3\; = \;m\;\] có đúng 2 nghiệm \[x \in \left( {1;3} \right)\;\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đặt \[t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)\]
Xét hàm số\[y = {t^2} - 8t + 3\] trên (2;8) có:
\[y' = 2t - 8;y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4 \in (2;8)\]
Bảng biến thiên:
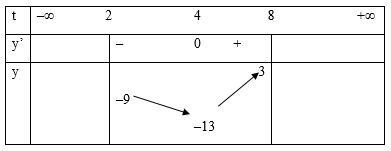
Căn cứ bảng biến thiên:
Phương trình \[{4^x} - {\rm{\;}}{2^{x{\rm{\;}} + {\rm{\;}}3}} + {\rm{\;}}3{\rm{\;}} = {\rm{\;}}m\] có đúng 2 nghiệm \[x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\]
Đáp án cần chọn là: A
Sách thầy cô Vietjack biên soạn:
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 290.000
₫ 140.000
Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1)
Đã bán 902
₫ 150.000
₫ 39.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1)
Đã bán 851
₫ 150.000
₫ 39.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tổng các nghiệm của phương trình \[{3^{{x^4} - 3{x^2}}} = 81\]
Xem đáp án »
27/06/2022
10,787
Câu 3:
Số nghiệm thực phân biệt của phương trình \[{2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} = 4\]là:
Xem đáp án »
27/06/2022
1,218
Câu 4:
Đề thi THPT QG - 2021 - mã 101
Có bao nhiêu số nguyên y sao cho tồn tại \[x \in (\frac{1}{3};3)\;\] thỏa mãn \[27{\,^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{9x}}\]?
Xem đáp án »
27/06/2022
1,196
Câu 5:
Phương trình \[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\] có tổng các nghiệm gần nhất với số nào dưới đây:
Xem đáp án »
27/06/2022
773
Câu 6:
Tìm tập hợp tất cả các nghiệm của phương trình \[{2^{{x^2} + x - 1}} = \frac{1}{2}\].
Xem đáp án »
27/06/2022
725
Câu 7:
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt: \[{9^{1 - x}} + 2(m - 1){3^{1 - x}} + 1 = 0\]
Xem đáp án »
27/06/2022
567
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận