Câu hỏi:
28/06/2022 149Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
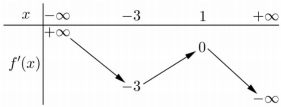
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
Đáp án chính xác
Câu hỏi trong đề:
ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bất phương trình mũ !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo đề bài ta có : \[f\left( x \right) < {e^x} + m \Leftrightarrow f\left( x \right) - {e^x} < m\]
Đặt\[g\left( x \right) = f\left( x \right) - {e^x}.\] Khi đó :
\[\begin{array}{l}f(x) < {e^x} + m\forall x \in ( - 1;1)\\ \Rightarrow g(x) = f(x) - {e^x} < m\forall x \in ( - 1;1)\\ \Leftrightarrow m \ge \mathop {max}\limits_{[ - 1;1]} g(x)\\g\prime (x) = f\prime (x) - {e^x}\end{array}\]
Trên (−1;1) ta có \[f'\left( x \right) < 0;\,\,{e^x} > 0\,\,\forall x \in R \Rightarrow g'\left( x \right) < 0\,\,\forall x \in \left( { - 1;1} \right)\]
⇒g(x) nghịch biến trên (−1;1).
\[\begin{array}{*{20}{l}}{ \Rightarrow \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \frac{1}{e}}\\{ \Rightarrow m \ge f\left( { - 1} \right) - \frac{1}{e}.}\end{array}\]
Đáp án cần chọn là: C
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
Xem đáp án »
28/06/2022
817
Câu 2:
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
Xem đáp án »
28/06/2022
589
Câu 3:
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
Xem đáp án »
28/06/2022
584
Câu 4:
Bất phương trình \[{\left( {\sqrt 2 } \right)^{{x^2} - 2x}} \le {\left( {\sqrt 2 } \right)^3}\]có tập nghiệm là:
Xem đáp án »
28/06/2022
473
Câu 5:
Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
Xem đáp án »
28/06/2022
341
Câu 6:
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
Xem đáp án »
28/06/2022
330
Câu 7:
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
Xem đáp án »
28/06/2022
314
Bình luận
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 5)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 4)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
về câu hỏi!