Biết rằng bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - 1 < 2x - 3}\\{\frac{{5 - 3x}}{2} < x - 3}\\{3x \le x + 5}\end{array}} \right.\) có tập nghiệm là một đoạn \[[a;b].\]Hỏi a + b bằng:
A.\[\frac{{11}}{2}.\]
B.8
C. \[\frac{9}{2}.\]
D. \[\frac{{47}}{{10}}.\]
Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Hệ bất phương trình !!
Quảng cáo
Trả lời:
Bất phương trình
\(\left\{ {\begin{array}{*{20}{c}}{x - 1 < 2x - 3}\\{5 - 3x < 2x - 6}\\{3x \le x + 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2 < x}\\{11 \le 5x}\\{2x \le 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x >2}\\{x \ge \frac{{11}}{5}}\\{x \le \frac{5}{2}}\end{array} \Leftrightarrow } \right.\frac{{11}}{5} \le x \le \frac{5}{2}\)
Suy ra \[a + b = \frac{{11}}{5} + \frac{5}{2} = \frac{{47}}{{10}}.\]
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\left( { - \frac{1}{4}; - 1} \right) \notin S\]
B.\[S = \left\{ {\left( {x;y} \right)|4x - 3y = 2} \right\}\]
C.Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d, với d là là đường thẳng 4x − 3y = 2.
D.Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d, với d là là đường thẳng 4x − 3y = 2.
Lời giải
Dễ thấy \[x = - \frac{1}{4};y = - 1\] thỏa mãn cả hai bất phương trình nên\[\left( { - \frac{1}{4}; - 1} \right) \in S\] do đó A sai.
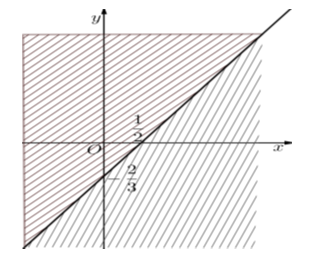
Ta sẽ biểu diễn tập nghiệm của bất phương trình trên mặt phẳng tọa độ như sau:
Trước hết, ta vẽ hai đường thẳng:
\[\left( {{d_1}} \right):2x - \frac{3}{2}y = 1\]
\[\left( {{d_2}} \right):4x - 3y = 2\]
Thử trực tiếp ta thấy (0;0) là nghiệm của bất phương trình (2) vì 4.0-3.0 < 2 (đúng)
Nhưng (0;0) không phải là nghiệm của bất phương trình (1) vì \[2.0 - \frac{3}{2}.0 < 1\]
Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng\[\left( d \right):4x - 3y = 2.\]
Đáp án cần chọn là: B
Câu 2
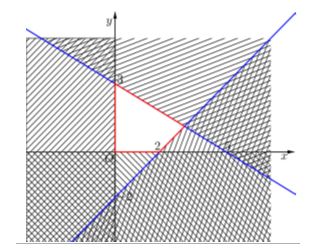
A.Trên mặt phẳng tọa độ Oxy, biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với \[A\left( {0;3} \right),B\left( {\frac{{25}}{8};\frac{9}{8}} \right),C\left( {2;0} \right)\] và O(0;0).
B.Đường thẳng \[\Delta :x + y = m\;\] luôn có giao điểm với miền nghiệm của hệ với mọi giá trị của m.
C.Giá trị lớn nhất của biểu thức x+y , với x và y thỏa mãn hệ bất phương trình đã cho là 174.
D.Giá trị nhỏ nhất của biểu thức x+y , với x và y thỏa mãn hệ bất phương trình đã cho là 0.
Lời giải
Trước hết, ta vẽ bốn đường thẳng:
\[\left( {{d_1}} \right):x - y = 2\]
\[\left( {{d_2}} \right):3x + 5y = 15\]
\[\left( {{d_3}} \right):x = 0\]
\[\left( {{d_4}} \right):y = 0\]
- Miền nghiệm là phần không bị gạch, kể cả biên nên A đúng.
- Đáp án B sai vì nếu m = 5 ta vẽ đường thẳng x + y = 5 sẽ không có giao điểm với miền nghiệm của hệ.
- Ta sẽ tìm GTLN, GTNN của biểu thức\[F\left( {x;y} \right) = x + y\] với (x;y) là nghiệm của hệ.
Ta có:
\[\begin{array}{*{20}{l}}{F\left( {0;3} \right) = 0 + 3 = 3,F\left( {\frac{{25}}{8};\frac{9}{8}} \right) = \frac{{25}}{8} + \frac{9}{8} = \frac{{17}}{4},}\\{F\left( {2;0} \right) = 2 + 0 = 2,F\left( {0;0} \right) = 0 + 0 = 0}\end{array}\]
Đáp án cần chọn là: B
Câu 3
A.\[S = \left( { - \infty ; - 3} \right).\]
B. \[S = \left( { - \infty ;2} \right).\]
C. \[S = \left( { - 3;2} \right).\]
D. \[S = \left( { - 3; + \infty } \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[S = \left( { - 2;\frac{4}{5}} \right).\]
B. \[S = \left( {\frac{4}{5}; + \infty } \right).\]
C. \[S = \left( { - \infty ; - 2} \right).\]
D. \[S = \left( { - 2; + \infty } \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[m < \frac{1}{3}.\]
B. \[0 \ne m < \frac{1}{3}.\]
C. \[m \ne 0.\]
D. m < 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.m>3
B.\[m \ge 3\].
C.m<3.
D.\[m \le 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.m>2
B.m=2 .
C.\[m \le 2\].
D. m < 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.