Cho tứ diện ABCD, gọi G là trọng tâm tam giác ACD, M thuộc đoạn thẳng BC sao cho CM=2MB. Chọn mệnh đề đúng trong các mệnh đề sau?

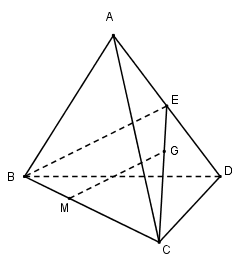
Gọi E là trung điểm của AB ta có:

\[\begin{array}{*{20}{l}}{M \in SE\,;\,\frac{{EM}}{{ES}} = \frac{1}{3}}\\{N \in EC\,;\,\frac{{EN}}{{EC}} = \frac{1}{3}}\end{array}\]

Xét tam giác ESC ta có\[\frac{{EM}}{{ES}} = \frac{{EN}}{{EC}} = \frac{1}{3}\]

\( \Rightarrow MN//SC\) (Định lí Ta – let đảo).

Mà \[SC \subset \left( {SCD} \right) \Rightarrow MN//(SCD)\]Đáp án cần chọn là: C

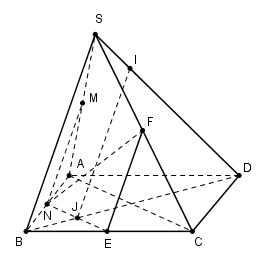
Trước hết ta lấy điểm \[M \in (P)\;\] sao cho \[M \in SA\].

Trong mp(SAB) kẻ MN // SA \[(N \in AB),\]trong mp(ABCD) kẻ NE // AC \[(E \in BC).\]

\[NE \cap BD = \left\{ J \right\}\]

Trong mp(SBC) kẻ EF // SB \[(F \in SC),\]trong mp(SBD) kẻ JI // SD \[(I \in SD).\]

Giả sử MN // (SCD)

Lại có: MN // SB⇒\[SB \subset \left( {SCD} \right)\] (vô lý) nên (1) sai.

Tương tự ta chứng minh được (2) sai.

\[ \subset \left( {SAC} \right) \Rightarrow \subset \left( {SAC} \right) \Rightarrow NE{\rm{ }}//{\rm{ }}\left( {SAC} \right).\;\]Do đó (3) đúng.

\[IJ{\rm{ }}//{\rm{ }}SB \subset \left( {SAB} \right) \Rightarrow IJ{\rm{ }}//{\rm{ }}\left( {SAB} \right).\]Do đó (4) đúng.

Đáp án cần chọn là: B