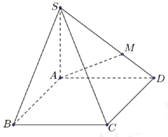
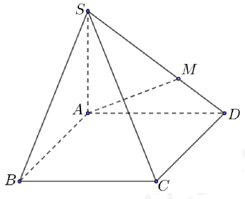
Cho tứ diện ABCD có AB=6, CD=8. Cắt tứ diện bởi một mặt phẳng song song với AB, CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng
A.\[\frac{{31}}{7}\]
B. \[\frac{{18}}{7}\]
C. \[\frac{{24}}{7}\]
D. \[\frac{{15}}{7}\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
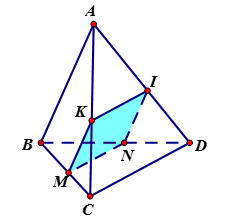
Giả sử một mặt phẳng song song với AB và CD cắt tứ diện ABCD theo một thiết diện là hình thoi MNIK như hình vẽ trên. Khi đó ta có:\(\left\{ {\begin{array}{*{20}{c}}{MK//AB//IN}\\{MN//CD//IK}\\{MK = KI}\end{array}} \right.\)
Cách 1: Theo định lí Ta – lét ta có:\(\left\{ {\begin{array}{*{20}{c}}{\frac{{MK}}{{AB}} = \frac{{CK}}{{AC}}}\\{\frac{{KI}}{{CD}} = \frac{{AK}}{{AC}}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{MK}}{6} = \frac{{AC - AK}}{{AC}}}\\{\frac{{KI}}{8} = \frac{{AK}}{{AC}}}\end{array}} \right.\)
\[ \Rightarrow \frac{{MK}}{6} = 1 - \frac{{AK}}{{AC}} \Rightarrow \frac{{MK}}{6} = 1 - \frac{{KI}}{8} \Rightarrow \frac{{MK}}{6} = 1 - \frac{{MK}}{8} \Leftrightarrow \frac{7}{{24}}MK = 1 \Leftrightarrow MK = \frac{{24}}{7}\]
Vậy hình thoi có cạnh bằng\[\frac{{24}}{7}\]
Đáp án cần chọn là: C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{1}{3}\]
B. \[\frac{2}{3}\]
C. \[\frac{1}{2}\]
D. \[\frac{3}{4}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
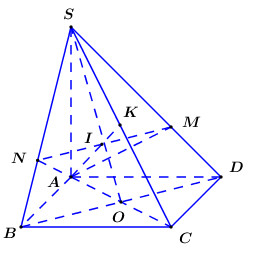
Gọi mặt phẳng chứa AM và song song với BD là (α).
Trong (SBD) kẻ\[MN//BD\,\,\left( {N \in SB} \right)\] khi đó ta có\[\left( \alpha \right) \equiv \left( {AMN} \right)\]
Gọi\[O = AC \cap BD\] trong (SBD) gọi \[\left\{ I \right\} = MN \cap SO\] trong (SAC) gọi\[K = AI \cap SC\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{K \in AI \subset (AMN)}\\{K \in SC}\end{array}} \right. \Rightarrow K = \left( {AMN} \right) \cap SC\) hay\[K = \left( \alpha \right) \cap SC\]
Áp dụng định lí Talets ta có\[\frac{{SI}}{{SO}} = \frac{{SM}}{{SD}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{IS}}{{IO}} = 2\]
Ta có: O là trung điểm của AC nên\[\frac{{AO}}{{AC}} = \frac{1}{2}\]
Áp dụng định lí Menelaus trong tam giác SOC, cát tuyến AIK ta có:
\[\frac{{IS}}{{IO}}.\frac{{AO}}{{AC}}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow 2.\frac{1}{2}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow \frac{{KC}}{{KS}} = 1 \Rightarrow \frac{{SK}}{{SC}} = \frac{1}{2}\]
Đáp án cần chọn là: C
Câu 2
A.\[T = \frac{3}{2}\]
b. \[T = \frac{1}{3}\]
C. \[T = 2\]
D. \[T = \frac{1}{2}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
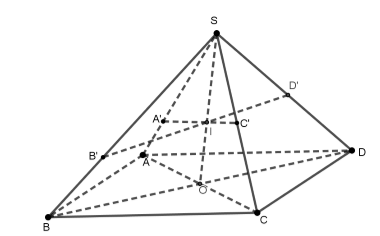
Gọi O là giao của AC và BD. Ta có O là trung điểm của đoạn thẳng AC, BD.
Các đoạn thẳng SO,A′C′, B′D′ đồng quy tại I.
Ta có: \[{S_{SA'I}} + {S_{SC'I}} = {S_{SA'C'}} \Leftrightarrow \frac{{{S_{SA'I}}}}{{{S_{SAC}}}} + \frac{{{S_{SC'I}}}}{{{S_{SAC}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{{S_{SA'I}}}}{{2{S_{SAO}}}} + \frac{{{S_{SC'I}}}}{{2{S_{SCO}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{SA'}}{{2SA}}.\frac{{SI}}{{SO}} + \frac{{SC'}}{{2SC}}.\frac{{SI}}{{SO}} = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}}\]
\[ \Leftrightarrow \frac{{SI}}{{2SO}}\left( {\frac{{SA'}}{{SA}} + \frac{{SC'}}{{SC}}} \right) = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}} \Leftrightarrow \frac{{SA}}{{SA'}} + \frac{{SC}}{{SC'}} = 2.\frac{{SO}}{{SI}}\]
Tương tự:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} = 2.\frac{{SO}}{{SI}}\]
Suy ra:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} - \frac{{SC}}{{SC'}} = \frac{{SA}}{{SA'}} = \frac{3}{2}\]
Đáp án cần chọn là: A
Câu 3
A.\[S = \frac{{17\sqrt 3 {a^2}}}{{18}}.\]
B. \[S = \frac{{5\sqrt 3 {a^2}}}{{18}}.\]
C. \[S = \frac{{13\sqrt 3 {a^2}}}{{18}}.\]
D. \[S = \frac{{11\sqrt 3 {a^2}}}{{18}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[AB = \frac{1}{3}CD\]
b. \[AB = \frac{3}{2}CD\]
c. \[AB = 3CD\]
d. \[AB = \frac{2}{3}CD\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.Tam giác.
B.Tứ giác.
C.Ngũ giác.
D.Lục giác
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\frac{1}{6}\]
b. \[\frac{1}{3}\]
c. \[\frac{5}{6}\]
d. \[\frac{2}{3}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập