ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bài toán thiết diện của hình chóp
59 người thi tuần này 4.6 2.3 K lượt thi 30 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 37)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2026 có đáp án (Đề số 2)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 36)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 35)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 30
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 29
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 34)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 28
Danh sách câu hỏi:
Câu 1
A.Hình tam giác
B.Hình thang
C.Hình bình hành
D.Hình chữ nhật
Lời giải
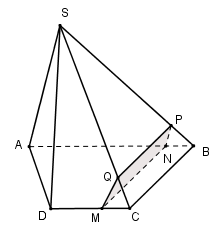
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{M \in (\alpha ) \cap (ABCD)}\\{BC\parallel (\alpha )}\\{BC \subset (ABCD)}\end{array}} \right. \Rightarrow (\alpha ) \cap (ABCD) = MN\parallel BC(N \in AB)\,\,(1)\)
Tương tự
\(\left\{ {\begin{array}{*{20}{c}}{N \in (\alpha ) \cap (SAB)}\\{SA\parallel (\alpha )}\\{SA \subset (SAB)}\end{array}} \right. \Rightarrow (\alpha ) \cap (SAB) = NP\parallel SA(P \in SB)\)
\(\left\{ {\begin{array}{*{20}{c}}{P \in (\alpha ) \cap (SBC)}\\{BC\parallel (\alpha )}\\{BC \subset (SBC)}\end{array}} \right. \Rightarrow (\alpha ) \cap (SBC) = PQ\parallel BC(Q \in SC)\,\,(2).\)
Từ (1) và (2) suy ra MN//PQ .
Vậy thiết diện là hình thang MNPQ.
Đáp án cần chọn là: B
Câu 2
A.d qua S và song song với BC
B.d qua S và song song với DC
C.d qua S và song song với AB
D.d qua S và song song với BD
Lời giải
Vì \[S \in \left( {SAD} \right)\] và\[S \in \left( {SBC} \right)\] nên\[S \in d\]
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{AD \subset (SAD)}\\{BC \subset (SBC)}\\{AD//BC}\\{d = (SAD) \cap (SBC)}\end{array}} \right. \Rightarrow d//AD//BC\)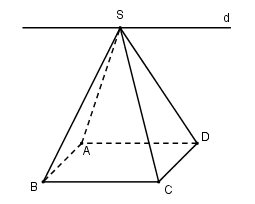
Đáp án cần chọn là: A
Câu 3
A.Hình tam giác
B.Hình vuông
C.Hình thoi
D.Hình chữ nhật
Lời giải
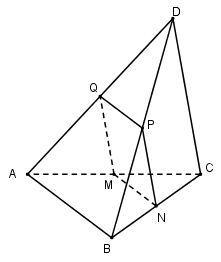
Gọi M là trung điểm của AC .
Trong (ABC) qua M kẻ \[MN//AB\left( {N \in BC} \right)\] Trong (ACD) và (BCD) kẻ MQ//CD và \[NP//CD\left( {Q \in AD,P \in BD} \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{M \in (\alpha ) \cap (ABC)}\\{AB \subset (ABC)}\\{AB//(\alpha )}\\{MN//AB}\end{array}} \right. \Rightarrow (\alpha ) \cap (ABC) = MN\)
Chứng minh tương tự ta có:\[\left( \alpha \right) \cap \left( {BCD} \right) = NP//CD\]
\[\begin{array}{*{20}{l}}{\left( \alpha \right) \cap \left( {ABD} \right) = PQ//AB}\\{\left( \alpha \right) \cap \left( {ACD} \right) = QM//CD.}\end{array}\]
Vậy thiết diện của hình chóp cắt bởi mp(α) là tứ giác MNPQ .
Ta có: \[MN//PQ//AB,MQ//NP//CD\] nên MNPQ là hình bình hành.
Ta có: MN là đường trung bình của tam giác ABC và MQ là đường trung bình của tam giác ACD nên\[MN = \frac{1}{2}AB,MQ = \frac{1}{2}CD.\]
Mà AB=CD nên MN=MQ . Vậy MNPQ là hình thoi.
Đáp án cần chọn là: C
Lời giải
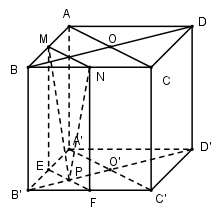
Ta có: MN là đường trung bình của tam giác ABC nên\[MN//AC//A'C'\]
(MNP) và (A′B′C′D′) có điểm P chung và MN//A′C′ .
Qua P kẻ \[EF//A'C';E \in A'B',F \in B'C'.\]
Vậy thiết diện của hình lập phương cắt bởi mp(MNP) là MNFE.
Đáp án cần chọn là: B
Câu 5
A.Là đường thẳng song song với AB
B.Là đường thẳng song song với CD
C.Là đường song song với đường trung bình của hình thang ABCD
D.Cả A, B, C đều đúng
Lời giải
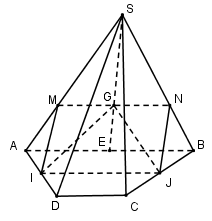
Ta có: ABCD là hình thang và I,J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD.
\[ \Rightarrow IJ//AB//CD\]
\(\left\{ {\begin{array}{*{20}{c}}{G \in (SAB) \cap (IJG)}\\{AB \subset (SAB)}\\{IJ \subset (IJG)}\\{AB//IJ}\end{array}} \right.\) Trong (SAB) qua G kẻ\[MN//AB\left( {M \in SA;N \in SB} \right)\]
\[ \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN\] và \[MN//IJ//AB//CD\]
Đáp án cần chọn là: D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[NB = \frac{1}{2}BC\]
B.\[\frac{{NB}}{{NC}} = \frac{1}{2}\]
C. \[\frac{{BN}}{{CN}} = 2\]
D. \[NC = \frac{1}{3}NB.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.Hình thang
B.Hình bình hành
C.Hình chữ nhật
D.Hình tam giác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A.MN và BC đồng phẳng
B.MN và BC song song với nhau
C.ABCD là hình thang và MN là đường trung bình của hình thang ABCDABCD
D.Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A.\[AB = \frac{2}{3}CD\]
B. \[AB = CD\]
C. \[AB = \frac{3}{2}CD\]
D. \[AB = 3CD\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A.Thẳng hàng
B.Cùng thuộc một đường tròn cố đinh.
C.Ba điểm tạo thành một tam giác
D.Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.Hình bình hành
B.Hình thoi
C.Hình thang
D.Hình thang cân
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A.4a
B.4a−m
C.4a−2m
D.2a+m
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A.Hình thoi
B.Hình bình hành
C.Tứ giác có các cạnh đối cắt nhau
D.Hình thang cân
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A.\[\frac{{2ab}}{3}\]
B. \[\frac{{2ab}}{9}\]
C. \[\frac{{ab}}{3}\]
D. \[\frac{{ab}}{9}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A.\[\frac{1}{3}\]
B. \[\frac{2}{3}\]
C. \[\frac{1}{2}\]
D. \[\frac{3}{4}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A.Tam giác.
B.Tứ giác.
C.Ngũ giác.
D.Lục giác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A.\[\frac{{31}}{7}\]
B. \[\frac{{18}}{7}\]
C. \[\frac{{24}}{7}\]
D. \[\frac{{15}}{7}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A.Ngũ giác
B.Tứ giác
C.Tam giác
D.Lục giác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A.\[AB = \frac{1}{3}CD\]
b. \[AB = \frac{3}{2}CD\]
c. \[AB = 3CD\]
d. \[AB = \frac{2}{3}CD\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A.\[\frac{3}{4}\]
b. \[\frac{1}{3}\]
c. \(\frac{1}{2}\)
d. \[\frac{2}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A.\[\frac{{9{a^2}\sqrt {139} }}{4}\]
B. \[\frac{{9{a^2}\sqrt {139} }}{8}\]
C. \[\frac{{9{a^2}\sqrt 7 }}{8}\]
D. \[\frac{{9{a^2}\sqrt {139} }}{{16}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A.\[\frac{1}{6}\]
b. \[\frac{1}{3}\]
c. \[\frac{5}{6}\]
d. \[\frac{2}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A.\(ab\)
B. \[\frac{{ab}}{9}\]
C. \(2ab\)
C. \[\frac{{2ab}}{9}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A.\[\frac{{5{a^2}\sqrt 3 }}{{18}}\]
B. \[\frac{{5{a^2}\sqrt 3 }}{6}\]
C. \[\frac{{4{a^2}\sqrt 3 }}{9}\]
D. \[\frac{{4{a^2}\sqrt 3 }}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A.\[\frac{{3\sqrt {15} {a^2}}}{{16}}\]
B. \[\frac{{3\sqrt 5 {a^2}}}{{16}}\]
C. \[\frac{{3\sqrt 5 {a^2}}}{8}\]
D. \[\frac{{\sqrt {15} {a^2}}}{{16}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A.\[S = \frac{{17\sqrt 3 {a^2}}}{{18}}.\]
B. \[S = \frac{{5\sqrt 3 {a^2}}}{{18}}.\]
C. \[S = \frac{{13\sqrt 3 {a^2}}}{{18}}.\]
D. \[S = \frac{{11\sqrt 3 {a^2}}}{{18}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A.\[T = \frac{3}{2}\]
b. \[T = \frac{1}{3}\]
C. \[T = 2\]
D. \[T = \frac{1}{2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.