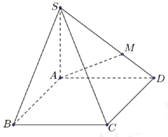
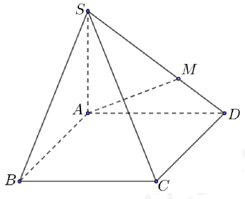
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA=SD=3a, SB=SC=\(3a\sqrt 3 \). Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP=2a. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP).
A.\[\frac{{9{a^2}\sqrt {139} }}{4}\]
B. \[\frac{{9{a^2}\sqrt {139} }}{8}\]
C. \[\frac{{9{a^2}\sqrt 7 }}{8}\]
D. \[\frac{{9{a^2}\sqrt {139} }}{{16}}\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
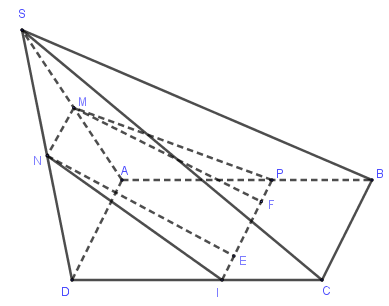
Do MN//AD⇒MN//BC. Vậy (MNP) cắt mặt phẳng (ABCD) theo giao tuyến đi qua P, song song BC và cắt DC tại điểm I. Thiết diện của khối chóp cắt bởi mặt phẳng (MNP) chính là hình thang MNIP.
Do \[\Delta NDI = \Delta MAP\;\] nên MP=NI. Từ đó suy ra MNIP là hình thang cân.
Trong tam giác SAB, ta có
\[\cos \widehat {SAB} = \frac{{S{A^2} + A{B^2} - S{B^2}}}{{2.SA.AB}} = \frac{{9{a^2} + 9{a^2} - 27{a^2}}}{{2.3a.3a}} = - \frac{{9{a^2}}}{{18{a^2}}} = - \frac{1}{2}\]
Trong tam giác MAP, ta có
\[M{P^2} = M{A^2} + A{P^2} - 2MA.AP.\cos \widehat {MAP} = \frac{{9{a^2}}}{4} + 4{a^2} + \frac{{3a}}{2} \cdot 2a = \frac{{37{a^2}}}{4} \Rightarrow MP = \frac{{a\sqrt {37} }}{2}\]
Từ M kẻ \[MF \bot PI\], từ N kẻ \[NE \bot PI\].
Dễ thấy, tứ giác MNEF là hình chữ nhật và từ đó suy ra
\[MN = EF = \frac{{3a}}{2} \Rightarrow PF = EI = \frac{{3a}}{4}\]
Xét tam giác vuông MFP, ta có
\[MF = \sqrt {M{P^2} - F{P^2}} = \sqrt {\frac{{37{a^2}}}{4} - \frac{{9{a^2}}}{{16}}} = \frac{{a\sqrt {139} }}{4}\]
Ta có
\[{S_{MNIP}} = \frac{{\left( {MN + IP} \right).MF}}{2} = \frac{{\left( {\frac{{3a}}{2} + 3a} \right) \cdot \frac{{a\sqrt {139} }}{4}}}{2} = \frac{{9{a^2}\sqrt {139} }}{{16}}\]
Đáp án cần chọn là: D
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{1}{3}\]
B. \[\frac{2}{3}\]
C. \[\frac{1}{2}\]
D. \[\frac{3}{4}\]
Lời giải
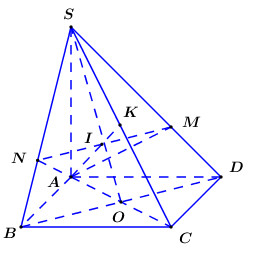
Gọi mặt phẳng chứa AM và song song với BD là (α).
Trong (SBD) kẻ\[MN//BD\,\,\left( {N \in SB} \right)\] khi đó ta có\[\left( \alpha \right) \equiv \left( {AMN} \right)\]
Gọi\[O = AC \cap BD\] trong (SBD) gọi \[\left\{ I \right\} = MN \cap SO\] trong (SAC) gọi\[K = AI \cap SC\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{K \in AI \subset (AMN)}\\{K \in SC}\end{array}} \right. \Rightarrow K = \left( {AMN} \right) \cap SC\) hay\[K = \left( \alpha \right) \cap SC\]
Áp dụng định lí Talets ta có\[\frac{{SI}}{{SO}} = \frac{{SM}}{{SD}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{IS}}{{IO}} = 2\]
Ta có: O là trung điểm của AC nên\[\frac{{AO}}{{AC}} = \frac{1}{2}\]
Áp dụng định lí Menelaus trong tam giác SOC, cát tuyến AIK ta có:
\[\frac{{IS}}{{IO}}.\frac{{AO}}{{AC}}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow 2.\frac{1}{2}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow \frac{{KC}}{{KS}} = 1 \Rightarrow \frac{{SK}}{{SC}} = \frac{1}{2}\]
Đáp án cần chọn là: C
Câu 2
A.\[T = \frac{3}{2}\]
b. \[T = \frac{1}{3}\]
C. \[T = 2\]
D. \[T = \frac{1}{2}\]
Lời giải
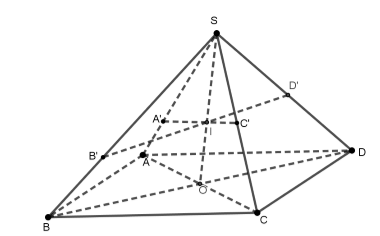
Gọi O là giao của AC và BD. Ta có O là trung điểm của đoạn thẳng AC, BD.
Các đoạn thẳng SO,A′C′, B′D′ đồng quy tại I.
Ta có: \[{S_{SA'I}} + {S_{SC'I}} = {S_{SA'C'}} \Leftrightarrow \frac{{{S_{SA'I}}}}{{{S_{SAC}}}} + \frac{{{S_{SC'I}}}}{{{S_{SAC}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{{S_{SA'I}}}}{{2{S_{SAO}}}} + \frac{{{S_{SC'I}}}}{{2{S_{SCO}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{SA'}}{{2SA}}.\frac{{SI}}{{SO}} + \frac{{SC'}}{{2SC}}.\frac{{SI}}{{SO}} = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}}\]
\[ \Leftrightarrow \frac{{SI}}{{2SO}}\left( {\frac{{SA'}}{{SA}} + \frac{{SC'}}{{SC}}} \right) = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}} \Leftrightarrow \frac{{SA}}{{SA'}} + \frac{{SC}}{{SC'}} = 2.\frac{{SO}}{{SI}}\]
Tương tự:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} = 2.\frac{{SO}}{{SI}}\]
Suy ra:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} - \frac{{SC}}{{SC'}} = \frac{{SA}}{{SA'}} = \frac{3}{2}\]
Đáp án cần chọn là: A
Câu 3
A.\[S = \frac{{17\sqrt 3 {a^2}}}{{18}}.\]
B. \[S = \frac{{5\sqrt 3 {a^2}}}{{18}}.\]
C. \[S = \frac{{13\sqrt 3 {a^2}}}{{18}}.\]
D. \[S = \frac{{11\sqrt 3 {a^2}}}{{18}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[AB = \frac{1}{3}CD\]
b. \[AB = \frac{3}{2}CD\]
c. \[AB = 3CD\]
d. \[AB = \frac{2}{3}CD\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[\frac{{31}}{7}\]
B. \[\frac{{18}}{7}\]
C. \[\frac{{24}}{7}\]
D. \[\frac{{15}}{7}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\frac{1}{6}\]
b. \[\frac{1}{3}\]
c. \[\frac{5}{6}\]
d. \[\frac{2}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[\frac{{3\sqrt {15} {a^2}}}{{16}}\]
B. \[\frac{{3\sqrt 5 {a^2}}}{{16}}\]
C. \[\frac{{3\sqrt 5 {a^2}}}{8}\]
D. \[\frac{{\sqrt {15} {a^2}}}{{16}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập