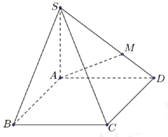
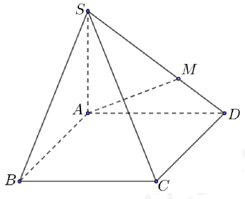
Cho tứ diện ABCD có AB=a, CD=b. Gọi I, J lần lượt là trung điểm AB và CD, giả sử AB⊥CD. Mặt phẳng (α) qua M nằm trên đoạn IJ và song song với AB và CD Tính diện tích thiết diện của tứ diện ABCD với mặt phẳng (α) biết \[IM = \frac{1}{3}IJ\].
A.\(ab\)
B. \[\frac{{ab}}{9}\]
C. \(2ab\)
C. \[\frac{{2ab}}{9}\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
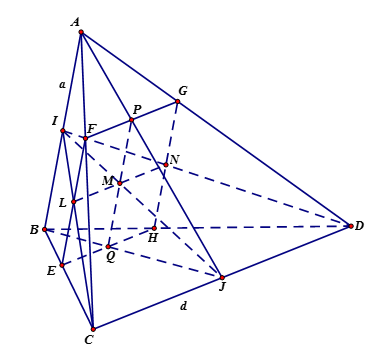
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (ICD)}\\{M \in (\alpha ) \cap (ICD)}\end{array}} \right.\) ⇒ giao tuyến của (α) với (ICD) là đường thẳng qua M và
song song với CDcắt IC tại L và ID tại N.
\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (JAB)}\\{M \in (\alpha ) \cap (JAB)}\end{array}} \right.\) ⇒ giao tuyến của (α) với (JAB) là đường thẳng qua M và song song
với AB cắt JA tại P và JB tại Q.
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (ABC)}\\{L \in (\alpha ) \cap (ABC)}\end{array}} \right. \Rightarrow EF//AB\,\,\,\,\left( 1 \right)\)
Tương tự \(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (ABD)}\\{N \in (\alpha ) \cap (ABD)}\end{array}} \right. \Rightarrow HG//AB\,\,\left( 2 \right)\)
Từ (1) và (2) \[ \Rightarrow EF//HG//AB\,\,\,\left( 3 \right)\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (ACD)}\\{P \in (\alpha ) \cap (ACD)}\end{array}} \right. \Rightarrow FG//CD\,\,\,\left( 4 \right)\)
Tương tự\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (BCD)}\\{Q \in (\alpha ) \cap (BCD)}\end{array}} \right. \Rightarrow EH//CD\,\,\,\left( 5 \right)\)
Từ (4) và (5) \[ \Rightarrow FG//EH//CD\,\,\,\,\left( 6 \right)\]
Từ (3) và (6), suy ra EFGH là hình bình hành. Mà AB⊥CD nên EFGH là hình chữ nhật.
Xét tam giác ICD có:\[LN//CD \Rightarrow \frac{{LN}}{{CD}} = \frac{{IN}}{{ID}}\]
Xét tam giác ICD có:\[MN//JD \Rightarrow \frac{{IN}}{{ID}} = \frac{{IM}}{{IJ}}\]
Do đó\[\frac{{LN}}{{CD}} = \frac{{IM}}{{IJ}} = \frac{1}{3} \Rightarrow LN = \frac{1}{3}CD = \frac{b}{3}\]
Tương tự\[\frac{{PQ}}{{AB}} = \frac{{JM}}{{JI}} = \frac{2}{3} \Rightarrow PQ = \frac{2}{3}AB = \frac{{2a}}{3}\]
Vậy\[{S_{EFGH}} = PQ.LN = \frac{{2ab}}{9}\]
Đáp án cần chọn là: D
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{1}{3}\]
B. \[\frac{2}{3}\]
C. \[\frac{1}{2}\]
D. \[\frac{3}{4}\]
Lời giải
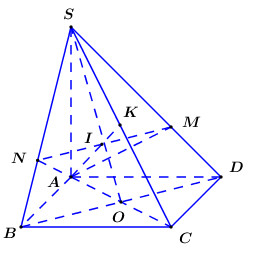
Gọi mặt phẳng chứa AM và song song với BD là (α).
Trong (SBD) kẻ\[MN//BD\,\,\left( {N \in SB} \right)\] khi đó ta có\[\left( \alpha \right) \equiv \left( {AMN} \right)\]
Gọi\[O = AC \cap BD\] trong (SBD) gọi \[\left\{ I \right\} = MN \cap SO\] trong (SAC) gọi\[K = AI \cap SC\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{K \in AI \subset (AMN)}\\{K \in SC}\end{array}} \right. \Rightarrow K = \left( {AMN} \right) \cap SC\) hay\[K = \left( \alpha \right) \cap SC\]
Áp dụng định lí Talets ta có\[\frac{{SI}}{{SO}} = \frac{{SM}}{{SD}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{IS}}{{IO}} = 2\]
Ta có: O là trung điểm của AC nên\[\frac{{AO}}{{AC}} = \frac{1}{2}\]
Áp dụng định lí Menelaus trong tam giác SOC, cát tuyến AIK ta có:
\[\frac{{IS}}{{IO}}.\frac{{AO}}{{AC}}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow 2.\frac{1}{2}.\frac{{KC}}{{KS}} = 1 \Leftrightarrow \frac{{KC}}{{KS}} = 1 \Rightarrow \frac{{SK}}{{SC}} = \frac{1}{2}\]
Đáp án cần chọn là: C
Câu 2
A.\[T = \frac{3}{2}\]
b. \[T = \frac{1}{3}\]
C. \[T = 2\]
D. \[T = \frac{1}{2}\]
Lời giải
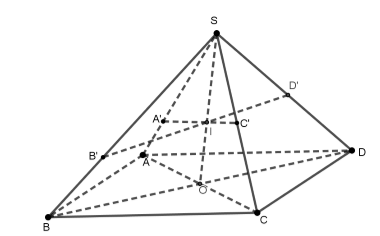
Gọi O là giao của AC và BD. Ta có O là trung điểm của đoạn thẳng AC, BD.
Các đoạn thẳng SO,A′C′, B′D′ đồng quy tại I.
Ta có: \[{S_{SA'I}} + {S_{SC'I}} = {S_{SA'C'}} \Leftrightarrow \frac{{{S_{SA'I}}}}{{{S_{SAC}}}} + \frac{{{S_{SC'I}}}}{{{S_{SAC}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{{S_{SA'I}}}}{{2{S_{SAO}}}} + \frac{{{S_{SC'I}}}}{{2{S_{SCO}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\]
\[ \Leftrightarrow \frac{{SA'}}{{2SA}}.\frac{{SI}}{{SO}} + \frac{{SC'}}{{2SC}}.\frac{{SI}}{{SO}} = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}}\]
\[ \Leftrightarrow \frac{{SI}}{{2SO}}\left( {\frac{{SA'}}{{SA}} + \frac{{SC'}}{{SC}}} \right) = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}} \Leftrightarrow \frac{{SA}}{{SA'}} + \frac{{SC}}{{SC'}} = 2.\frac{{SO}}{{SI}}\]
Tương tự:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} = 2.\frac{{SO}}{{SI}}\]
Suy ra:\[\frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} - \frac{{SC}}{{SC'}} = \frac{{SA}}{{SA'}} = \frac{3}{2}\]
Đáp án cần chọn là: A
Câu 3
A.\[S = \frac{{17\sqrt 3 {a^2}}}{{18}}.\]
B. \[S = \frac{{5\sqrt 3 {a^2}}}{{18}}.\]
C. \[S = \frac{{13\sqrt 3 {a^2}}}{{18}}.\]
D. \[S = \frac{{11\sqrt 3 {a^2}}}{{18}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[AB = \frac{1}{3}CD\]
b. \[AB = \frac{3}{2}CD\]
c. \[AB = 3CD\]
d. \[AB = \frac{2}{3}CD\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[\frac{{31}}{7}\]
B. \[\frac{{18}}{7}\]
C. \[\frac{{24}}{7}\]
D. \[\frac{{15}}{7}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\frac{{3\sqrt {15} {a^2}}}{{16}}\]
B. \[\frac{{3\sqrt 5 {a^2}}}{{16}}\]
C. \[\frac{{3\sqrt 5 {a^2}}}{8}\]
D. \[\frac{{\sqrt {15} {a^2}}}{{16}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.Tam giác.
B.Tứ giác.
C.Ngũ giác.
D.Lục giác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo