Cho tứ diện ABCD có AB vuông góc với CD. Mặt phẳng (P) song song với AB và CD lần lượt cắt BC,DB,AD,AC tại M,N,P,Q. Tứ giác MNPQ là hình gì?
A.Hình thang
B.Hình bình hành
C.Hình chữ nhật
D.Hình vuông
Quảng cáo
Trả lời:
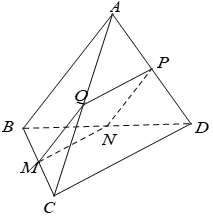
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(MNPQ)//AB}\\{(MNPQ) \cap (ABC) = MQ}\end{array}} \right. \Rightarrow MQ//AB\)
Tương tự ta có:\[MN//CD,\,\,NP//AB,\,\,QP//C{\rm{D}}\]
Do đó tứ giác MNPQ là hình bình hành
lại có\[MN \bot MQ\left( {do\,AB \bot CD\,} \right)\]
Vậy tứ giác MNPQ là hình chữ nhật.
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.300.
B.450.
C.600.
D.\({90^0}\)
Lời giải
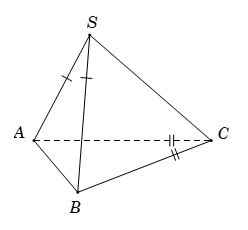
Xét \[\overrightarrow {SC} .\overrightarrow {AB} = - \overrightarrow {CS} .\left( {\overrightarrow {CB} - \overrightarrow {CA} } \right) = \overrightarrow {CS} .\overrightarrow {CA} - \overrightarrow {CS} .\overrightarrow {CB} \]
\[ = CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB}\]
Do \[{\rm{\Delta }}SAC = {\rm{\Delta }}SBC\left( {c.c.c} \right)\]nên\[\widehat {SCA} = \widehat {SCB} \Rightarrow \cos \widehat {SCA} = \cos \widehat {SCB}\]
Do đó\[CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB} = 0\](do \[CA = CB\]) hay\[\overrightarrow {SC} .\overrightarrow {AB} = 0\]
Vậy \[SC \bot AB\]
Đáp án cần chọn là: DCâu 7. Mệnh đề nào sau đây là đúng?
A.Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B.Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau
C.Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau
D.Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đáp án cần chọn là: D
Câu 2
A.\[\left| {\vec a + \vec b} \right| = \sqrt {19} \]
B. \[\left| {\vec a - \vec b} \right| = 7\]
C. \[\left| {\vec a - 2\vec b} \right| = \sqrt {139} \]
D. \[\left| {\vec a + 2\vec b} \right| = 9\]
Lời giải
\[ = {\left| {\vec a} \right|^2} + {\left| {\vec b} \right|^2} + 2.\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right) = {3^2} + {5^2} + 2.3.5.\left( { - \frac{1}{2}} \right) = 19\]
Do đó\[\left| {\vec a + \vec b} \right| = \sqrt {19} \]
Đáp án B:\[{\left| {\vec a - \vec b} \right|^2} = {\left( {\vec a - \vec b} \right)^2} = {\vec a^2} - 2\vec a\vec b + {\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} - 2.\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right) + {\left| {\vec b} \right|^2} = {3^2} - 2.3.5.\left( { - \frac{1}{2}} \right) + {5^2} = 49\]
\[ \Rightarrow \left| {\vec a - \vec b} \right| = 7\]nên B đúng.
Đáp án C:\[{\left| {\vec a - 2\vec b} \right|^2} = {\left( {\vec a - 2\vec b} \right)^2} = {\vec a^2} - 4\vec a\vec b + 4{\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} - 4\left| {\vec a} \right|\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) + 4{\left| {\vec b} \right|^2} = {3^2} - 4.3.5.\left( { - \frac{1}{2}} \right) + {4.5^2} = 139\]
\[ \Rightarrow \left| {\vec a - 2\vec b} \right| = \sqrt {139} \]nên C đúng.
Đáp án D:\[{\left| {\vec a + 2\vec b} \right|^2} = {\left( {\vec a + 2\vec b} \right)^2} = {\vec a^2} + 4\vec a\vec b + 4{\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} + 4\left| {\vec a} \right|\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) + 4{\left| {\vec b} \right|^2} = {3^2} + 4.3.5.\left( { - \frac{1}{2}} \right) + {4.5^2} = 79\]
\[ \Rightarrow \left| {\vec a + 2\vec b} \right| = \sqrt {79} \]nên D sai.
Đáp án cần chọn là: D
Câu 3
A.\[{60^0}\]
B. \[{90^0}\]
C. \[{45^0}\]
D. \[{30^0}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[{45^ \circ }\]
B. \[{30^ \circ }\]
C. \[{90^ \circ }\]
D. \[{60^ \circ }\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[{60^0}.\]
B. \[{30^0}.\]
C. \[{90^0}.\]
D. \[{45^0}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[{90^0}\]
B. \[{60^0}\]
C. \[{45^0}\]
D. \[{120^0}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.