Cho hình chóp S.ABCD có \[SA \bot \left( {ABCD} \right),\] đáy ABCD là hình thoi cạnh bằng a và \(\widehat B = {60^0}\)Biết SA=2a. Tính khoảng cách từ A đến SC.
A.\[\frac{{3a\sqrt 2 }}{2}\]
B. \[\frac{{4a\sqrt 3 }}{3}\]
C. \[\frac{{2a\sqrt 5 }}{5}\]
D. \[\frac{{5a\sqrt 6 }}{2}\]
Quảng cáo
Trả lời:
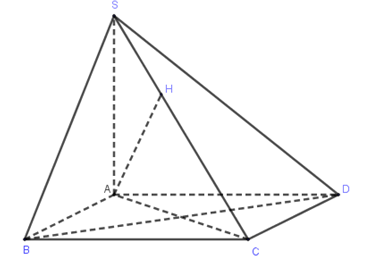
Kẻ \[AH \bot SC\] khi đó \[d\left( {A,SC} \right) = AH\]
ABCD là hình thoi cạnh bằng a và\[\hat B = {60^ \circ } \Rightarrow {\rm{\Delta }}ABC\] đều nên\[AC = a\]
Trong tam giác vuông SAC ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}}\]
\[ \Rightarrow AH = \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \frac{{2\sqrt 5 a}}{5}\]
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.2a
B.\[\sqrt 3 a\]
C. 0
D. \(\sqrt 2 a\)
Lời giải
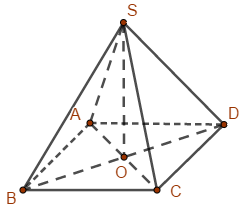
Bước 1:
Gọi O là giao điểm của AC và BD.
S.ABCD là hình chóp đều nên O là hình chiếu của S lên (ABCD).
\[d\left( {S,\left( {ABCD} \right)} \right) = SO\]
Bước 2:
ABCD là hình vuông nên
\[\begin{array}{*{20}{l}}{AC = a\sqrt 2 .\sqrt 2 = 2a = > AO = a}\\{ = > S{O^2} = S{A^2} - A{O^2} = 2{a^2} - {a^2} = {a^2}}\\{ = > SO = a}\end{array}\]
Đáp án cần chọn là: C
Câu 2
A.2a.
B.\[a\sqrt 3 .\]
C.a.
D.\[a\sqrt 5 .\]
Lời giải
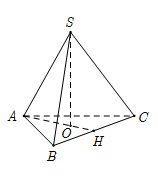
Gọi O là chân đường cao của hình chóp nên O là tâm tam giác đáy.
Do đó O là trọng tâm tam giác ABC hay\[O \in AH\]
Ta có \[AO = \frac{2}{3}AH = \frac{2}{3}.3a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \]
\[{\rm{d}}\left( {S,AH} \right) = SO = \sqrt {S{A^2} - A{O^2}} = a\]Đáp án cần chọn là: C
Câu 3
A.\[\frac{{a\sqrt 5 }}{2}\]
B. \[2a\sqrt 5 \]
C. \[a\sqrt 2 \]
D. \[\frac{{a\sqrt 3 }}{2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.A′,B,C′.
B.B,C,D.
C.B′,C′,D′.
D.A,A′,D′.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[\sqrt 2 .\]
B.\[\sqrt 3 .\]
C. 2
D. \[\frac{{\sqrt 3 }}{2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[a\sqrt 2 \]
B. \[\frac{{a\sqrt 6 }}{2}\]
C. \[\frac{{a\sqrt 3 }}{2}\]
D. \[\frac{{a\sqrt 6 }}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[a\sqrt 2 \]
B. \[2a\]
C. \[2a\sqrt 3 \]
D. \[a\sqrt 3 \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.