ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Khoảng cách từ một điểm đến một đường thẳng
71 người thi tuần này 4.6 2 K lượt thi 13 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 37)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2026 có đáp án (Đề số 2)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 36)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 35)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 30
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 29
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 34)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 28
Danh sách câu hỏi:
Câu 1
A.\[\sqrt 2 .\]
B.\[\sqrt 3 .\]
C. 2
D. \[\frac{{\sqrt 3 }}{2}.\]
Lời giải
Do\(\left\{ {\begin{array}{*{20}{c}}{SA \bot AB}\\{SA \bot BC}\end{array}} \right.\) nên\[SA \bot (ABC) \Rightarrow SA \bot AC\]
Như vậy \[SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + A{B^2} + B{C^2}} = \sqrt 3 \]
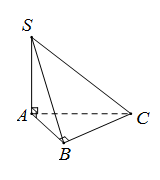
Đáp án cần chọn là: B
Câu 2
A.\[a\sqrt {\frac{7}{5}} .\]
B. \[a\sqrt {\frac{4}{7}} .\]
C. \[a\sqrt {\frac{6}{{11}}} .\]
D. \[a\sqrt {\frac{2}{3}} .\]
Lời giải
Dựng hình chiếu H của C trên AM
Do \[\Delta BCD\] đều cạnh aa nên đường cao \[MC = \frac{{a\sqrt 3 }}{2}\]
\[d\left( {C,AM} \right) = CH = \frac{{AC.MC}}{{\sqrt {A{C^2} + M{C^2}} }} = \frac{{a\sqrt {66} }}{{11}}\]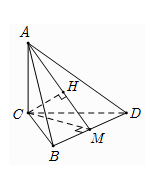
Đáp án cần chọn là: C
Câu 3
A.2a.
B.\[a\sqrt 3 .\]
C.a.
D.\[a\sqrt 5 .\]
Lời giải
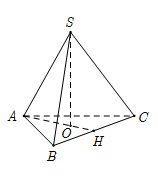
Gọi O là chân đường cao của hình chóp nên O là tâm tam giác đáy.
Do đó O là trọng tâm tam giác ABC hay\[O \in AH\]
Ta có \[AO = \frac{2}{3}AH = \frac{2}{3}.3a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \]
\[{\rm{d}}\left( {S,AH} \right) = SO = \sqrt {S{A^2} - A{O^2}} = a\]Đáp án cần chọn là: C
Câu 4
A.\[\frac{{3a\sqrt 2 }}{2}\]
B. \[\frac{{2a\sqrt 3 }}{3}\]
C. \[\frac{{4a\sqrt 5 }}{3}\]
D. \[\frac{{a\sqrt {11} }}{2}\]
Lời giải
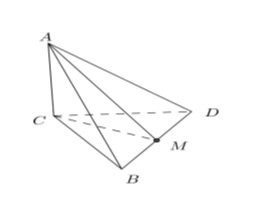
Gọi M là trung điểm của BD.
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{AC \bot BD}\\{CM \bot BD}\end{array}} \right. \Rightarrow BD \bot AM\) (Định lý 3 đường vuông góc)
\[ \Rightarrow d\left( {A;BD} \right) = AM\]
\[CM = \frac{{a\sqrt 3 }}{2}\] (vì tam giác BCD đều).
Ta có: \[AM = \sqrt {A{C^2} + M{C^2}} = \sqrt {2{a^2} + \frac{{3{a^2}}}{4}} = \frac{{a\sqrt {11} }}{2}\]
Đáp án cần chọn là: D
Câu 5
A.\[\frac{{3a\sqrt 2 }}{2}\]
B. \[\frac{{4a\sqrt 3 }}{3}\]
C. \[\frac{{2a\sqrt 5 }}{5}\]
D. \[\frac{{5a\sqrt 6 }}{2}\]
Lời giải
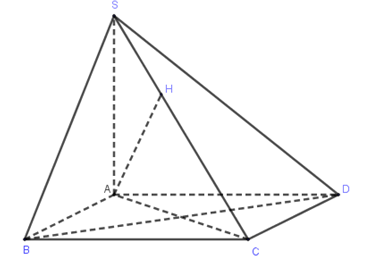
Kẻ \[AH \bot SC\] khi đó \[d\left( {A,SC} \right) = AH\]
ABCD là hình thoi cạnh bằng a và\[\hat B = {60^ \circ } \Rightarrow {\rm{\Delta }}ABC\] đều nên\[AC = a\]
Trong tam giác vuông SAC ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}}\]
\[ \Rightarrow AH = \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \frac{{2\sqrt 5 a}}{5}\]
Đáp án cần chọn là: C
Câu 6
A.\[a\sqrt 2 \]
B. \[\frac{{a\sqrt 6 }}{2}\]
C. \[\frac{{a\sqrt 3 }}{2}\]
D. \[\frac{{a\sqrt 6 }}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[\frac{{a\sqrt 5 }}{2}\]
B. \[2a\sqrt 5 \]
C. \[a\sqrt 2 \]
D. \[\frac{{a\sqrt 3 }}{2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.\[\frac{{a\sqrt 3 }}{3}\]
B. \[\frac{{a\sqrt 3 }}{4}\]
C. \[\frac{{a\sqrt 2 }}{3}\]
D. \[\frac{{a\sqrt 2 }}{4}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A.\[a\sqrt 2 \cot \alpha \]
B. \[a\sqrt 2 \tan \alpha \]
C. \[\frac{{a\sqrt 2 }}{2}{\rm{cos}}\alpha \]
D. \[\frac{{a\sqrt 2 }}{2}\sin \alpha \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A.2a
B.\[\sqrt 3 a\]
C. 0
D. \(\sqrt 2 a\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A.\[\frac{{3a\sqrt 2 }}{2}\]
B. \[\frac{{7a\sqrt 5 }}{5}\]
C. \[\frac{{8a\sqrt 3 }}{3}\]
D. \[\frac{{5a\sqrt 6 }}{6}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A.\[a\sqrt 2 \]
B. \[2a\]
C. \[2a\sqrt 3 \]
D. \[a\sqrt 3 \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.A′,B,C′.
B.B,C,D.
C.B′,C′,D′.
D.A,A′,D′.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.