Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty Bảo Việt với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12 triệu đồng với lãi suất hàng năm không đổi là 6% / năm. Hỏi sau đúng 18 năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân.
A.403,32 (triệu đồng).
B.293,32 (triệu đồng).
C.412,23 (triệu đồng).
D.393,12 (triệu đồng).
Quảng cáo
Trả lời:
Gọi số tiền đóng hàng năm là A=12 (triệu đồng), lãi suất là\[r = 6{\rm{\% }} = 0,06\]
Sau 1 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là\[{A_1} = A\left( {1 + r} \right)\] (nhưng người đó không rút mà lại đóng thêm A triệu đồng nữa, nên số tiền gốc để tính lãi năm sau là\[{A_1} + A\])
Sau 2 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_2} = \left( {{A_1} + A} \right)\left( {1 + r} \right) = \left[ {A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right) = A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Sau 3 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[\begin{array}{l}{A_3} = \left( {{A_2} + A} \right)\left( {1 + r} \right) = \left[ {A{{\left( {1 + r} \right)}^2} + A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right)\\ = A{\left( {1 + r} \right)^3} + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\end{array}\]
Sau 18 năm, người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_{18}} = A{\left( {1 + r} \right)^{18}} + A{\left( {1 + r} \right)^{17}} + ... + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Tính:\[{A_{18}} = A\left[ {{{\left( {1 + r} \right)}^{18}} + {{\left( {1 + r} \right)}^{17}} + ... + {{\left( {1 + r} \right)}^2} + \left( {1 + r} \right) + 1 - 1} \right]\]
\[ \Rightarrow {A_{18}} = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{{\left( {1 + r} \right) - 1}} - 1} \right] = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{r} - 1} \right] = 12\left[ {\frac{{{{\left( {1 + 0,06} \right)}^{19}} - 1}}{{0,06}} - 1} \right] \approx 393,12\]
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bước 1: Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] và tìm điều kiện xác định.
Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] (coi yy là tham số).
Điều kiện xác định của f(x) là:
\(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} > 0}\\{{y^2} + y + 64 > 0}\\{x - y > 0}\end{array}} \right.\)
Do x,y nguyên nên\[x > y \ge - {y^2}\] Cũng vì x,y nguyên nên ta chỉ xét f(x) trên nửa khoảng \[\left[ {y + 1; + \infty } \right)\]
Bước 2: Xét hàm số trên\[\left[ {y + 1; + \infty } \right)\]
Ta có:
\[f'\left( x \right) = \frac{1}{{\left( {x + {y^2}} \right)\ln 2020}} - \frac{1}{{\left( {x - y} \right)\ln 2021}} - \frac{1}{{\left( {x - y} \right)\ln 4}} < 0,\;\forall x \ge y + 1\]
Bước 3: Lập bảng biến thiên
Ta có bảng biến thiên của hàm số f(x):
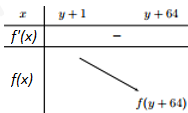
Bước 4: Tìm y nguyên \[f\left( {y + 64} \right) < 0\]
Yêu cầu bài toán trở thành:
\[f\left( {y + 64} \right) < 0\]
\[ \Leftrightarrow {\log _{2020}}\left( {{y^2} + y + 64} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) < {\log _4}64\]
\[ \Leftrightarrow {\log _{2021}}\left( {{y^2} + y + 64} \right)\left( {{{\log }_{2020}}2021 + 1} \right) < 3\]
\[ \Leftrightarrow {y^2} + y + 64 - {2021^{\frac{3}{{{{\log }_{2020}}2021 + 1}}}} < 0\]
\[ \Leftrightarrow - 301,76 < y < 300,76\]
Mà y nguyên nên\[y \in \left\{ { - 301; - 300; \ldots ;299;300} \right\}\]
Vậy có 602 giá trị nguyên của yy thỏa mãn yêu cầu.
Câu 2
Tập nghiệm của bất phương trình \[\log \left( {{x^2} + 25} \right) > \log \left( {10x} \right)\] là:
A.\[R \setminus \left\{ 5 \right\}\]
B. \[\left( {0;5} \right) \cup \left( {5; + \infty } \right)\]
C. R
D. \[\left( {0; + \infty } \right)\]
Lời giải
Điều kiện:\[x > 0\]
\[\log ({x^2} + 25) > \log (10x) \Leftrightarrow {x^2} + 25 > 10x \Leftrightarrow {(x - 5)^2} > 0 \Leftrightarrow x \ne 5\]
Tập nghiệm của bất phương trình là:\[(0;5) \cup (5; + \infty )\]
Đáp án cần chọn là: B
Câu 3
A.\[m \in \left( {0; + \infty } \right)\]
B. \[m \in \left( { - \frac{3}{4};0} \right)\]
C. \[m \in \left( { - \frac{3}{4}; + \infty } \right)\]
D. \[m \in \left( { - \infty ;0} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[S = ( - 2;0) \cup (\frac{1}{3};\,\,3\,]\]
B. \[S = ( - 1;0) \cup (\frac{1}{3};\,\,2\,]\,.\]
C. \[S = \left[ { - 1\,,\,0} \right) \cup (\frac{1}{3};\,\,3\,]\]
D. \[S = ( - 1;0) \cup (1;\,\,3\,]\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.