Câu hỏi:
11/07/2024 864Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích V=6m3 dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng \(\frac{2}{9}\) diện tích nắp bể. Biết rằng chi phí cho 1m2 bê tông cốt thép là 1.000.000d. Tính chi phí thấp nhất mà cô Ngọc phải trả khi xây bể (làm tròn đến hàng trăm nghìn và các chữ số viết liền)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
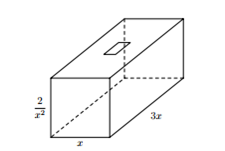
Bước 1: Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể. Tính chiều cao của bể.
Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể, h là chiều cao của bể.
Theo bài ra ta có: \[V = x.3x.h = 6 \Rightarrow h = \frac{6}{{3{x^2}}} = \frac{2}{{{x^2}}}\,\,\left( m \right)\]
Bước 2: Tính tổng diện tích các mặt làm bê tông.
Khi đó tổng diện tích các mặt bể được làm bê tông là:
\[2x.\frac{2}{{{x^2}}} + 2.3x.\frac{2}{{{x^2}}} + 2x.3x - x.3x.\frac{2}{9} = \frac{{16{x^2}}}{3} + \frac{{16}}{x}\]
Bước 3: Sử dụng BĐT Cô-si cho 3 số dương để tính số tiền ít nhất cần tìm
Áp dụng BĐT Cô-si ta có:
\[\frac{{16{x^2}}}{3} + \frac{{16}}{x} = \frac{{16{x^2}}}{3} + \frac{8}{x} + \frac{8}{x} \ge 3\sqrt[3]{{\frac{{16{x^2}}}{3}.\frac{8}{x}.\frac{8}{x}}} = 8\sqrt[3]{{18}}\]
Dấu “=” xảy ra khi\[\frac{{16{x^2}}}{3} = \frac{8}{x} \Leftrightarrow x = \sqrt[3]{{\frac{3}{2}}}\]
Vậy số tiền ít nhất mà cô Ngọc cần bỏ ra là \[8\sqrt[3]{{18}}{.10^6} \approx 21.000.000d\]
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có\[y' = \cos x \Rightarrow y' = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\]
Do\[x \in \left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]\]nên\[k = - 1\]hay\[x = - \frac{\pi }{2}\]
Suy ra
\[y( - \frac{\pi }{2}) = - 1;y( - \frac{\pi }{3}) = - \frac{{\sqrt 3 }}{2}\]
\(\left\{ {\begin{array}{*{20}{c}}{\mathop {\max }\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]} y = - \frac{{\sqrt 3 }}{2}}\\{\mathop {\min }\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]} y = - 1}\end{array}} \right.\)
Đáp án cần chọn là: B
Lời giải
TXĐ: \[R \setminus \left\{ 0 \right\}\]
\[y' = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\]
\[y' = 0 \Leftrightarrow \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x = 1(tm)\]hoặc\[x = - 1(ktm)\]
Bảng biến thiên:
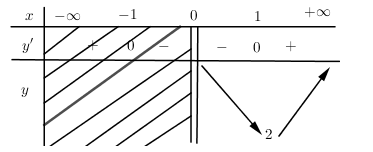
\[ \Rightarrow \mathop {Min}\limits_{x \in \left( {0; + \infty } \right)} \,y = f\left( 1 \right) = 2\]
Đáp án cần chọn là: A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Nhắn tin Zalo